福建省2021年数学中考定心卷
试卷更新日期:2021-09-30 类型:中考模拟
一、单选题
-
1. 在实数-3,-1,0,2中,比-2小的数是( )A、-3 B、-1 C、0 D、22. 五个大小相同的正方体搭成的几何体如图所示,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 2021年3月26日,国家航天局发布两幅由“天问一号”探测器拍摄的南、北半球火星侧身影像,该影像是探测器飞行至距离火星1.1万千米处,利用中分辨率相机拍摄的,将1.1万用科学记数法表示为( )A、 B、 C、 D、5. 如图,有理数 、 、 、 在数轴上的对应点分别是 、 、 、 ,若 ,则 的值( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 2021年3月26日,国家航天局发布两幅由“天问一号”探测器拍摄的南、北半球火星侧身影像,该影像是探测器飞行至距离火星1.1万千米处,利用中分辨率相机拍摄的,将1.1万用科学记数法表示为( )A、 B、 C、 D、5. 如图,有理数 、 、 、 在数轴上的对应点分别是 、 、 、 ,若 ,则 的值( )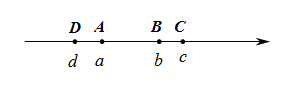 A、大于0 B、小于0 C、等于0 D、不确定6. 如图,在 中, , ,延长 到点 ,使 ,若 是 的中点,则 的长为( )
A、大于0 B、小于0 C、等于0 D、不确定6. 如图,在 中, , ,延长 到点 ,使 ,若 是 的中点,则 的长为( ) A、 B、 C、 D、17. 在 中, , 为对角线 上不同的两点,下列条件中,不能得出四边形 一定为平行四边形的是( )A、 B、 C、 D、8. 我国古代的数学著作《九章算术》中有下列问题:今有女子善织,日自倍,五日织五尺,问日织几何?其意思为:今有一女子很会织布,每日加倍增长,5日共织布5尺,问每日各织多少布?设她第一天织布 尺,则下面所列方程正确的是( )A、 B、 C、 D、9. 如图,点 , , 在 上, , ,连接 交 于点 ,则 的度数是( )
A、 B、 C、 D、17. 在 中, , 为对角线 上不同的两点,下列条件中,不能得出四边形 一定为平行四边形的是( )A、 B、 C、 D、8. 我国古代的数学著作《九章算术》中有下列问题:今有女子善织,日自倍,五日织五尺,问日织几何?其意思为:今有一女子很会织布,每日加倍增长,5日共织布5尺,问每日各织多少布?设她第一天织布 尺,则下面所列方程正确的是( )A、 B、 C、 D、9. 如图,点 , , 在 上, , ,连接 交 于点 ,则 的度数是( ) A、108° B、109° C、110° D、112°10. 已知二次函数 ,当 时,函数的最小值为 ;当 时,函数的最小值为 ,则 的值是( )A、-2 B、1 C、2 D、-2或2
A、108° B、109° C、110° D、112°10. 已知二次函数 ,当 时,函数的最小值为 ;当 时,函数的最小值为 ,则 的值是( )A、-2 B、1 C、2 D、-2或2二、填空题
-
11. 计算: .12. 已知一个等腰三角形的一个外角为82°,则这个等腰三角形的底角为.13. 已知 , ,计算 的值为.14. 一艘轮船只有在涨潮的时候才能驶入港口,已知该港口每天涨潮的时间为早上5:00至7:00和下午5:00至6:00,则该艘轮船在一昼夜内可以进港的概率是.15. 如图,正五边形 的边长为4,两条对角线 与 相交于 点,以 点为圆心, 长为半径画弧交 于 点,则图中阴影部分的面积为.(结果保留 )
 16. 已知直线 交双曲线 于 , 两点,交 轴于点 .若 ,则 的值是.
16. 已知直线 交双曲线 于 , 两点,交 轴于点 .若 ,则 的值是.三、解答题
-
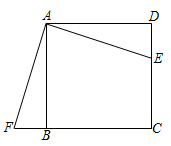
17. 解不等式组:18. 如图,点 在正方形 的边 上, 为 延长线上一点,且 ,连接 , .求证: .
 19. 先化简,再求值: ,其中 .20. 第四届数字中国建设峰会于2021年4月25-26日在福州举行,“福建特产”助力福州打动中国,某特产公司为峰会设计手工礼品,投入 元.若以2包茉莉花茶和1件脱胎漆器作为一份礼品,则刚好可制作600份礼品;若以1包茉莉花茶和3件脱胎漆器作为一份礼品,则刚好可制作400份礼品.(1)、若 ,求1包茉莉花茶与1件脱胎漆器的制作成本各是多少?(2)、若把 元钱全部用于制作茉莉花茶,总共可以制作多少包茉莉花茶?21. 如图,在 中, , , .
19. 先化简,再求值: ,其中 .20. 第四届数字中国建设峰会于2021年4月25-26日在福州举行,“福建特产”助力福州打动中国,某特产公司为峰会设计手工礼品,投入 元.若以2包茉莉花茶和1件脱胎漆器作为一份礼品,则刚好可制作600份礼品;若以1包茉莉花茶和3件脱胎漆器作为一份礼品,则刚好可制作400份礼品.(1)、若 ,求1包茉莉花茶与1件脱胎漆器的制作成本各是多少?(2)、若把 元钱全部用于制作茉莉花茶,总共可以制作多少包茉莉花茶?21. 如图,在 中, , , . (1)、在边 上求作一点 ,使 ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,求 的长.22. “让几千万农村贫困人口生活好起来,是我心中的牵挂.”习近平总书记多次对精准扶贫、精准脱贫作出重要指示.某村为脱贫致富,种植了脐橙,根据套袋情况估计,大约会收获100000个脐橙.现从脐橙树上随机摘下100个脐橙进行测重,统计单个脐橙的重量,得到如下图所示的频数分布直方图.
(1)、在边 上求作一点 ,使 ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,求 的长.22. “让几千万农村贫困人口生活好起来,是我心中的牵挂.”习近平总书记多次对精准扶贫、精准脱贫作出重要指示.某村为脱贫致富,种植了脐橙,根据套袋情况估计,大约会收获100000个脐橙.现从脐橙树上随机摘下100个脐橙进行测重,统计单个脐橙的重量,得到如下图所示的频数分布直方图.
根据频数分布直方图,解答下列问题:
(1)、以各组数据的中间数值代表这组数据的平均水平,求单个脐橙的平均重量;(2)、经销商与该村签订了脐橙收购协议,现有两种装箱方案:方案一:将脐橙采用随机混装的方式装箱,每箱装有脐橙10千克,每箱70元;
方案二:将脐橙按下表的一、二、三等级标准分别装箱,每箱50个,
价格如表所示:
等级
一等品
二等品
三等品
单个脐橙重量(克)
价格(元/箱)
180
120
60
根据所学知识判断,该村采用哪种方案装箱更合适,并说明理由.
23. 如图,在 中, ,以 为直径的 交 边于点 , 为 中点,连接 .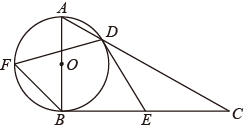 (1)、求证: 与 相切;(2)、 为 的中点,连接 , ,若 , ,求劣弧 的长.24. 如图①,在 和 中, , , .现将 绕着点 旋转一定角度后,再平移线段 得到线段 (点 与点 对应),连接 , .
(1)、求证: 与 相切;(2)、 为 的中点,连接 , ,若 , ,求劣弧 的长.24. 如图①,在 和 中, , , .现将 绕着点 旋转一定角度后,再平移线段 得到线段 (点 与点 对应),连接 , . (1)、如图②,当点 在线段 的延长线上时,求线段 的长;(2)、当点 与点 在直线 的同侧时,探究 与 的数量关系和位置关系,并说明理由;(3)、连接 ,求线段 长的最大值.25. 已知抛物线 的顶点为 ,点 为第三象限抛物线上的一点,过 点作直线 , 交抛物线于 , 两点(点 在点 的左侧), 交 轴于 点,连接 .(1)、当 , 两点在 轴上,且 为等腰直角三角形时,求 的值;(2)、当 经过 点, 经过 的中点 ,且 时,设直线 交 轴于 点,求证: 为 的中点;(3)、若 的内心在直线 上,设 的中点为 ,直线 经过 点且垂直于 轴,直线 经过 , 两点,记 与 的交点为 ,求证 点在一条新抛物线上,并求这条抛物线的解析式.
(1)、如图②,当点 在线段 的延长线上时,求线段 的长;(2)、当点 与点 在直线 的同侧时,探究 与 的数量关系和位置关系,并说明理由;(3)、连接 ,求线段 长的最大值.25. 已知抛物线 的顶点为 ,点 为第三象限抛物线上的一点,过 点作直线 , 交抛物线于 , 两点(点 在点 的左侧), 交 轴于 点,连接 .(1)、当 , 两点在 轴上,且 为等腰直角三角形时,求 的值;(2)、当 经过 点, 经过 的中点 ,且 时,设直线 交 轴于 点,求证: 为 的中点;(3)、若 的内心在直线 上,设 的中点为 ,直线 经过 点且垂直于 轴,直线 经过 , 两点,记 与 的交点为 ,求证 点在一条新抛物线上,并求这条抛物线的解析式.