四川省成都市2021-2022学年九年级上学期数学开学试卷
试卷更新日期:2021-09-30 类型:开学考试
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. 下列疫情防控标识图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 ,则下列不等式不一定成立的是( )A、 B、 C、 D、3. 下列由左边到右边的变形中,是因式分解的为( )A、 B、 C、 D、4. 若关于 的分式方程 有增根,则 的值为( )A、1 B、0 C、-2 D、-15. 如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A、6 B、7 C、8 D、96. 一次函数 的图象如图,则不等式 的解集为( )
2. 若 ,则下列不等式不一定成立的是( )A、 B、 C、 D、3. 下列由左边到右边的变形中,是因式分解的为( )A、 B、 C、 D、4. 若关于 的分式方程 有增根,则 的值为( )A、1 B、0 C、-2 D、-15. 如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A、6 B、7 C、8 D、96. 一次函数 的图象如图,则不等式 的解集为( )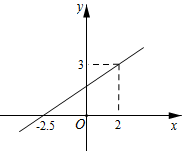 A、 B、 C、 D、7. 如图,直线 ,直线 和 被 , , 所截,如果 , , ,那么 的长是( )
A、 B、 C、 D、7. 如图,直线 ,直线 和 被 , , 所截,如果 , , ,那么 的长是( )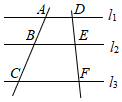 A、 B、 C、 D、8. 下列说法正确的是( )A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等且互相平分的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形9. 如图,在菱形ABCD中,AB=5、AC= 8,则该菱形的面积为( )
A、 B、 C、 D、8. 下列说法正确的是( )A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等且互相平分的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形9. 如图,在菱形ABCD中,AB=5、AC= 8,则该菱形的面积为( )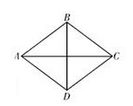 A、40 B、20 C、48 D、2410. 如图,矩形 中,连接 ,延长 至点 ,使 ,连接 .若 ,则 的度数是( )
A、40 B、20 C、48 D、2410. 如图,矩形 中,连接 ,延长 至点 ,使 ,连接 .若 ,则 的度数是( )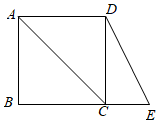 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)
-
11. 分解因式: .12. 若分式 , .13. 如图, 沿 所在直线向右平移得到 ,若 , ,则 .
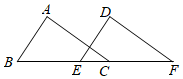 14. 如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以 , 为圆心,大于 的长为半径画弧,两弧交于 点,作射线 交边 于点 .若 , ,则 的面积是 .
14. 如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以 , 为圆心,大于 的长为半径画弧,两弧交于 点,作射线 交边 于点 .若 , ,则 的面积是 .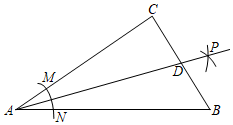
三、解答题(本大题共6个小题,共54分.)
-
15.(1)、分解因式: ;(2)、解方程: .16. 解不等式组: ,并把它的解集在数轴上表示出来.
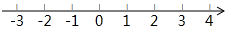 17. 先化简,再求值: ,在0,1, ,2这四个数中选一个合适的数代入求值.18. 如图,在平面直角坐标系中, 的顶点坐标分别为 , , .
17. 先化简,再求值: ,在0,1, ,2这四个数中选一个合适的数代入求值.18. 如图,在平面直角坐标系中, 的顶点坐标分别为 , , .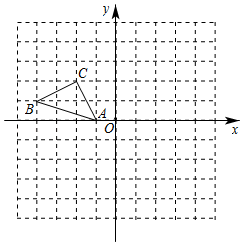
( 1 )直接写出点 关于原点对称的点 的坐标:;
( 2 )平移 ,使平移后点 的对应点 的坐标为 ,请画出平移后的△ ;
( 3 )画出 绕原点 逆时针旋转 后得到的△ .
19. 如图,在 中, 平分 交 于 ,作 交 于点 ,作 交 于点 .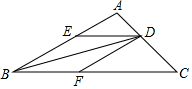 (1)、求证:四边形 是菱形;(2)、若 , , ,求菱形 的周长.20. 已知正方形 中,点 是边 上一点(不与 、 重合),将 绕点 顺时针旋转 得到 ,如图1,连接 ,分别交 、 于点 、 .
(1)、求证:四边形 是菱形;(2)、若 , , ,求菱形 的周长.20. 已知正方形 中,点 是边 上一点(不与 、 重合),将 绕点 顺时针旋转 得到 ,如图1,连接 ,分别交 、 于点 、 .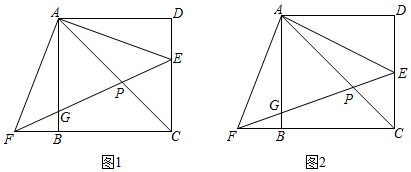 (1)、求证: ;(2)、求证: ;(3)、如图2,当点 是边 的中点时, ,求 的长.
(1)、求证: ;(2)、求证: ;(3)、如图2,当点 是边 的中点时, ,求 的长.四、填空题(本大题共5个小题,每小题4分,共20分。)
-
21. 若 ,则 .22. 若 是方程 的根,则 .23. 如图, 是 的边 的中点, 平分 ,且 ,垂足为 ,且 , , ,则 的周长是.
 24. 若关于 的一元一次不等式组 的解集为 ,且关于 的分式方程 有非负整数解,则符合条件的所有整数 的和为.25. 如图,在矩形 中, , ,点 是边 的中点,连接 ,将 沿 折叠得到 , 与 交于点 ,则 的长为.
24. 若关于 的一元一次不等式组 的解集为 ,且关于 的分式方程 有非负整数解,则符合条件的所有整数 的和为.25. 如图,在矩形 中, , ,点 是边 的中点,连接 ,将 沿 折叠得到 , 与 交于点 ,则 的长为.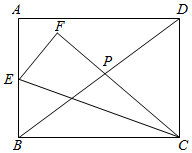
五、解答题(本大题共3个小题,共30分。)
-
26. 为做好新冠疫情的防控工作,某学校需购买甲、乙两种消毒液共50箱.经了解,每箱甲消毒液的售价比每箱乙消毒液的售价贵40元,且用1200元购买甲消毒液的数量恰好与用960元购买乙消毒液的数量相同.(1)、每箱甲、乙消毒液的售价分别是多少元?(2)、若两种消毒液都购买,且购买乙消毒液的箱数不多于甲消毒液箱数的 ,请问甲、乙消毒液分别购买多少箱时,所需总费用最少?最少总费用是多少?27. 正方形 和正方形 的边长分别为6和2,将正方形 绕点 逆时针旋转.
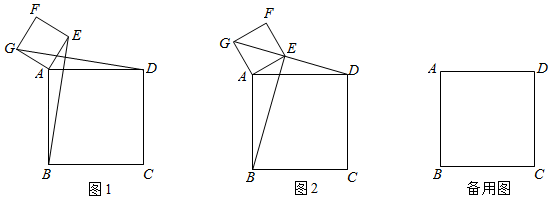 (1)、当旋转至图1位置时,连接 , ,线段 和 有何关系?请说明理由;(2)、在图1中,连接 , , ,请直接写出在旋转过程中 的面积最大值;(3)、在旋转过程中,当点 , , 在同一直线上时,请求出线段 的长.28. 如图,在矩形 中,点 在 轴上,点 在 轴上,点 坐标为 .矩形 沿直线 折叠,使点 落在对角线 上的 处,折痕与 、 轴分别交于点 、 .
(1)、当旋转至图1位置时,连接 , ,线段 和 有何关系?请说明理由;(2)、在图1中,连接 , , ,请直接写出在旋转过程中 的面积最大值;(3)、在旋转过程中,当点 , , 在同一直线上时,请求出线段 的长.28. 如图,在矩形 中,点 在 轴上,点 在 轴上,点 坐标为 .矩形 沿直线 折叠,使点 落在对角线 上的 处,折痕与 、 轴分别交于点 、 .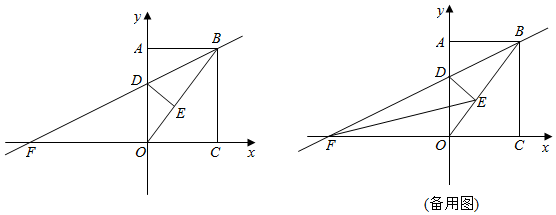 (1)、求点 的坐标;(2)、在直线 上找一点 ,使 的面积是 面积的两倍,求点 的坐标;(3)、连接 ,在第二象限是否存在点 ,使得 是等腰直角三角形.若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求点 的坐标;(2)、在直线 上找一点 ,使 的面积是 面积的两倍,求点 的坐标;(3)、连接 ,在第二象限是否存在点 ,使得 是等腰直角三角形.若存在,请直接写出点 的坐标;若不存在,请说明理由.