湖南省常德市澧县2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-30 类型：期中考试

进入出卷网下载

一、单选题

1. 下列说法中，①当k＞0时，反比例函数y＝ $\frac{k}{x}$ 的函数值y随x的增大而减小；②反比例函数y＝ $\frac{1}{x}$ ，当x＞1时，0＜y＜1；③相似三角形的面积比等于相似比； ④两个等腰三角形一定相似；⑤一元二次方程x²+5x＝﹣10，有两个不等实数根.其中正确的有（）个.

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 双曲线y＝ $\frac{2 k - 1}{x}$ 的图象经过第二、四象限，则k的取值范围是（）

A、k> $\frac{1}{2}$ B、k< $\frac{1}{2}$ C、k＝ $\frac{1}{2}$ D、不存在

查看试题解析
3. 直线y＝ax+b与双曲线y＝ $\frac{c}{x}$ 的图象，如图所示，则（）

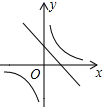A、a＞0，b＞0，c＞0 B、a＜0，b＜0，c＜0 C、a＜0，b＞0，c＞0 D、a＜0，b＜0，c＞0

查看试题解析
4. 下列方程中，是一元二次方程的是（）

A、x²+ $\frac{1}{x^{2}}$ ＝0 B、ax²+bx+c＝0 C、（x﹣1）（x﹣2）＝1 D、3x²﹣2xy﹣5y²＝0

查看试题解析
5. 若关于x的一元二次方程 $x^{2} + m x + n = 0$ 的两根分别为 $x_{1} = 2 ， x_{2} = 1$ ，则 $m ， n$ 的值分别是（）.

A、－3，2 B、3，－2 C、2，－3 D、2，3

查看试题解析
6. 若 $P$ 是 $Rt Δ ABC$ 斜边 $B C$ 上异于 $B$ ， $C$ 的一点，过点 $P$ 作直线截 $Δ A B C$ ，截得的三角形与原 $Δ A B C$ 相似，满足这样条件的直线有（）条.

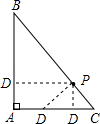A、1 B、2 C、3 D、4

查看试题解析
7. 如图，DE∥BC，DF∥AC，则下列比例式中正确的是（）

A、 $\frac{A D}{D B} = \frac{D E}{B C}$ B、 $\frac{A E}{E C} = \frac{B F}{F C}$ C、 $\frac{D F}{A C} = \frac{D E}{B C}$ D、 $\frac{E C}{A C} = \frac{B F}{B C}$

查看试题解析
8.
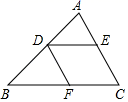反比例函数y= $\frac{a}{x}$ （a＞0，a为常数）和y= $\frac{2}{x}$ 在第一象限内的图象如图所示，点M在y= $\frac{a}{x}$ 的图象上，MC⊥x轴于点C，交y= $\frac{2}{x}$ 的图象于点A；MD⊥y轴于点D，交y= $\frac{2}{x}$ 的图象于点B，当点M在y= $\frac{a}{x}$ 的图象上运动时，以下结论：
①S_△_ODB=S_△_OCA；
②四边形OAMB的面积不变；
③当点A是MC的中点时，则点B是MD的中点．
其中正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

9. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点（1，-2），则k= ．

查看试题解析
10. 如图是三个反比例函数y＝ $\frac{k_{1}}{x}$ ，y＝ $\frac{k_{2}}{x}$ ，y＝ $\frac{k_{3}}{x}$ 在x轴上方的图象，由此观察得到k₁ ， k₂ ， k₃的大小关系为.

查看试题解析
11. 若m是方程2x²﹣3x﹣1＝0的一个根，则2020﹣6m²+9m的值为.

查看试题解析
12. 某种商品原价是100元，经两次降价后的价格是85元，求平均每次降价的百分率.设平均每次降价的百分率为x，可列方程为.

查看试题解析
13. 今年上半年，新冠病毒席卷全世界.已知某种病毒的直径为21.7微米（1毫米＝1000微米），用科学记数法表示这种病毒的直径为米.

查看试题解析
14. 已知实数a、b满足等式a²﹣2a﹣1＝0，b²﹣2b﹣1＝0，则 $\frac{b}{a} + \frac{a}{b}$ 的值是.

查看试题解析
15. 在平行四边形ABCD中，点E在直线AD上，AD＝3AE，连接CE交BD于点F，则EF：FC的值为.

查看试题解析
16. 如图，P为线段AB上一点，AD与BC交于点E，∠CPD＝∠A＝∠B，BC交PD于点F，AD交PC于点G，则图中相似三角形有对.

查看试题解析

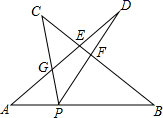
三、解答题

17. 解方程： $2 x^{2} - 5 x + 3 = 0$ .

查看试题解析
18. m（m+8）＝25.

查看试题解析
19. 等腰△ABC中，BC＝8，AB、AC的长是关于x的方程x²﹣10x+m＝0的两根，求m的值.

查看试题解析
20. 如图，DE∥BC，且DB＝AE，若AB＝5，AC＝10，求AE的长.

查看试题解析
21. 以长为2的线段为边作正方形ABCD，取AB的中点P，连接PD，在BA的延长线上取点F，使PF＝PD，以AF为边作正方形AMEF，点M在AD上，如图所示.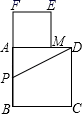

(1)、求AM、DM的长；

(2)、求证：AM²＝AD•DM.

查看试题解析
22. 某商店从厂家以每件21元的价格购进一批商品。若每件商品的售价为 $x$ 元，则可卖出 $(350 - 10 x)$ 件，但物价局限定每件商品的售价不能超过进价的120%。若该商店计划从这批商品中获取400元利润（不计其他成本），问需要卖出多少件商品，此时的售价是多少？

查看试题解析
23. 如图，在直角坐标系中，O为坐标原点.已知反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ）的图象经过点A（2，m），过点A作AB⊥x轴于点B，且△AOB的面积为 $\frac{1}{2}$ .

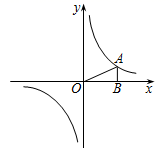(1)、求k和m的值；

(2)、点C（x，y）在反比例函数 $y = \frac{k}{x}$ 的图象上，求当1≤x≤3时，函数值y的取值范围.

查看试题解析
24. 如图，在△ABC中，AB＝8cm，BC＝16cm，点P从点A开始沿AB向B以2cm/s的速度移动，点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P，Q分别从A，B同时出发，经过几秒钟△PBQ与△ABC相似？

查看试题解析
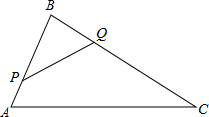25. 如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点.

(1)、求证：AC²＝AB•AD；

(2)、求证：CE∥AD；

(3)、若AD＝4，AB＝6，
①求 $\frac{D F}{D E}$ 的值；

②求DE的长.

查看试题解析
26. 如图，∠AOB＝90°，AB∥x轴，OB＝2，双曲线y＝ $\frac{k}{x}$ 经过点B，将△AOB绕点B逆时针旋转，使点O的对应点D落在x轴正半轴上，若AB的对应线段CB恰好经过点O.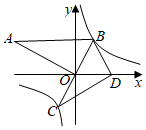

(1)、求点B坐标及双曲线解析式.

(2)、判断点C是否在双曲线上，请说明理由.

(3)、在y轴上是否存在一点P，使△PBD的周长最小，若存在，求点P的坐标；若不存在，请说明理由.

查看试题解析