湖北省宜昌市五峰土家族自治县2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-30 类型：期中考试

进入出卷网下载

一、单选题

1. 在天气预报图上，有各种各样表示天气的符号，下列表示天气符号的图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图△ABC绕点A旋转至△ADE，则旋转角是（）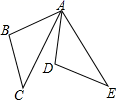

A、∠BAD B、∠BAC C、∠BAE D、∠CAD

查看试题解析
3. 根据下面表格中的取值，方程x²+x﹣3=0有一个根的近似值（精确到0.1）是（）
x
1.2
1.3
1.4
1.5
x²+x﹣3
﹣0.36
﹣0.01
0.36
0.75

A、1.5 B、1.2 C、1.3 D、1.4

查看试题解析
4. 如图所示，体育课上，小丽的铅球成绩为6.4m，她投出的铅球落在（）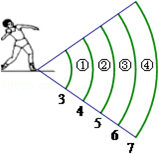

A、区域① B、区域② C、区域③ D、区域④

查看试题解析
5. 若x=5是方程 $x^{2} - 3 x + m = 0$ 的一个根，则m的值是（）

A、-5 B、5 C、10 D、-10

查看试题解析
6. 已知⊙O中最长的弦为8cm，则⊙O的半径为（）cm．

A、2 B、4 C、8 D、16

查看试题解析
7. 抛物线 $y = 2 x^{2} + c$ 的顶点坐标为(0，1)，则抛物线的解析式为（）

A、 $y = 2 x^{2} + 1$ B、 $y = 2 x^{2} - 1$ C、 $y = 2 x^{2} + 2$ D、 $y = 2 x^{2} - 2$

查看试题解析
8. 方程 $x^{2} + 6 x - 5 = 0$ 的左边配成完全平方后所得方程为（）

A、 ${(x + 3)}^{2} = 14$ B、 ${(x - 3)}^{2} = 14$ C、 ${(x + 3)}^{2} = 4$ D、 ${(x - 3)}^{2} = 4$

查看试题解析
9. 一元二次方程x²﹣2x=0的两根分别为x₁和x₂ ，则x₁x₂为（　　）

A、﹣2 B、1 C、2 D、0

查看试题解析
10. 若抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴的两个交点坐标是（－1，0）和（2，0），则此抛物线的对称轴是直线（）

A、 $x = - 1$ B、 $x = - \frac{1}{2}$ C、 $x = \frac{1}{2}$ D、 $x = 1$

查看试题解析
11. 已知函数y＝ax²+bx+c的图象如图所示，那么关于x的方程 $a x^{2} + b x + c 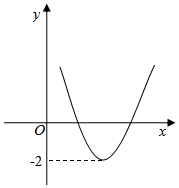+ \frac{3}{2} = 0$ 的根的情况是（）

A、无实数根 B、有两个相等实数根 C、有两个异号实数根 D、有两个同号不等实数根

查看试题解析

二、填空题

12. 写出一个开口向下的二次函数的表达式.

查看试题解析
13. 已知圆心角∠BOC＝100°，则对应的圆周角∠BAC的度数为.

查看试题解析
14. 点 $A (- 4 ， 1)$ 关于原点对称点 $A'$ 的坐标是.

查看试题解析
15. $《$ 田亩比类乘除捷法 $》$ 是我国古代数学家杨辉的著作，其中有一个数学问题：“直田积六十步，只云长阔共十六步，问长多阔几何”.意思是：一块矩形田地的面积为60平方步，只知道它的长与宽共16步，根据题意得，设长为x步，列出方程.

查看试题解析

三、解答题

16. 解方程：x(x－2)＋x－2＝0.

查看试题解析
17. 画出下列图形关于点O对称的图形.

查看试题解析
18. 已知抛物线y=ax²经过点A（-2，-8）.

(1)、求此抛物线的解析式；

(2)、判断点B（-1，-4）是否在此抛物线上；

(3)、求此抛物线上纵坐标为-6的点的坐标.

查看试题解析
19. 如图，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图所示，如果AF=4，AB=7，求：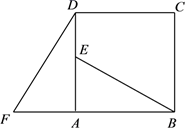

(1)、指出旋转中心和旋转角度；

(2)、求DE的长度；

(3)、BE与DF的位置关系如何？

查看试题解析
20. 已知二次函数 $y = {(x - 2)}^{2} - 1$ ，

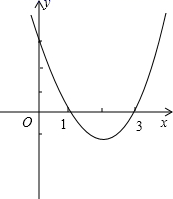(1)、确定抛物线开口方向、对称轴、顶点坐标；

(2)、如图，观察图象确定，x取什么值时，①y＞0，②y＜0，③y＝0.

查看试题解析
21. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后， $Δ A B C$ 的顶点均在格点上，点B的坐标为 $(1 ， 0)$ .

（ 1 ）画出 $Δ A B C$ 关于x轴对称的 $Δ A_{1} B_{1} C_{1}$ ，写出 $C_{1}$ 点的坐标；

（ 2 ）画出将 $Δ A B C$ 绕原点O按逆时针旋转 $90 °$ 所得的 $Δ A_{2} B_{2} C_{2}$ ，写出 $B_{2}$ 点的坐标并求出A运动经过的路径的长度.

查看试题解析
22. 如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N.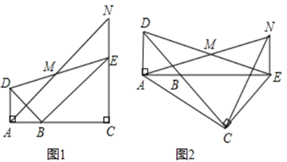

(1)、当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；

(2)、将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形.

查看试题解析
23. 诗词是中国人最经典的情感表达方式，也是民族生存延续的命脉.为了弘扬诗词国学，我校开展了“经典咏流传”的活动.轻拨经典的琴弦，我们将国家、民族、文化的美好精神文化传承下来，赋予经典文化以时代的灵魂.现我校初二（1）班为参加“经典咏流传”活动，班委会准备租赁演出服装、购买部分道具供班级集体使用.

(1)、班委会通过多方比较，决定用500元在A商店租赁服装，用300元在B商店购买道具.已知租赁一套服装比购买一套道具贵30元，同时所需道具比所需服装多5套，则初二（1）班班委会租赁了多少套演出服装、购买了多少套道具？

(2)、因后期参赛节目人员的调整，需要租赁更多的服装，购买更多的道具.经初步统计，最终需要租赁的演出服装套数比（1）中的演出服装套数增加了5a%（a＜60），道具套数比（1）中的道具套数增加了2a%.初二（1）班班委会需要再次租赁服装和购买道具，又前去与A商店、B商店议价，两个商店都在原来的售价上给予了a%的优惠，这次租赁服装和购买道具总共用了279元，求a的值.

查看试题解析
24. 已知二次函数y=mx²+(1﹣2m)x+1﹣3m ．

(1)、当m=2时，求二次函数图象的顶点坐标；

(2)、已知抛物线与x轴交于不同的点A、B ．
①求m的取值范围；

②若3≤m≤4时，求线段AB的最大值及此时二次函数的表达式．

查看试题解析

x	1.2	1.3	1.4	1.5
x²+x﹣3	﹣0.36	﹣0.01	0.36	0.75