湖北省孝感市孝南区2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-30 类型:期中考试
一、单选题
-
1. 下列手机手势解锁图案中,是中心对称图形的是( )A、
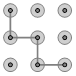 B、
B、 C、
C、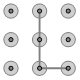 D、
D、 2. 一元二次方程x -4x-4=0配方后可化为( )A、(x-2) =4 B、(x-2) =8 C、(x-4) =4 D、(x-4) =83. 关于 的一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定4. 抛物线 的顶点坐标是( )A、 B、 C、 D、5. 如图,在△ABC中,AB= ,AC= ,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( )
2. 一元二次方程x -4x-4=0配方后可化为( )A、(x-2) =4 B、(x-2) =8 C、(x-4) =4 D、(x-4) =83. 关于 的一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定4. 抛物线 的顶点坐标是( )A、 B、 C、 D、5. 如图,在△ABC中,AB= ,AC= ,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( ) A、3 B、2 C、2 D、46. 若点 与 关于原点对称,则直线 不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 我区高效课堂建设确定以“信息技术与课堂教学深度融合”为抓手,加强对教师队伍建设的投入,计划从2020年起三年共投入3640万元,已知2020年投入1000万元,设投入经费的年平均增长率为 ,根据题意,下面所列方程正确的是( )A、 B、 C、 D、8. 若要得到函数 的图象,只需将函数 的图象( )A、先向右平移2个单位长度,再向上平移3个单位长度 B、先向左平移2个单位长度,再向上平移3个单位长度 C、先向左平移2个单位长度,再向下平移3个单位长度 D、先向右平移2个单位长度,再向下平移3个单位长度9. 如图,等腰 中, ,AC与正方形DEFG的的边长DE在同一直线上, ,开始时点C与点D重合,让 沿直线DE向右平移,到点A与点E重合时停止.设CD的长为x , 与正方形DEFG重合部分的面积为y , 则能表示y与x之间关系的图象大致是( ).
A、3 B、2 C、2 D、46. 若点 与 关于原点对称,则直线 不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 我区高效课堂建设确定以“信息技术与课堂教学深度融合”为抓手,加强对教师队伍建设的投入,计划从2020年起三年共投入3640万元,已知2020年投入1000万元,设投入经费的年平均增长率为 ,根据题意,下面所列方程正确的是( )A、 B、 C、 D、8. 若要得到函数 的图象,只需将函数 的图象( )A、先向右平移2个单位长度,再向上平移3个单位长度 B、先向左平移2个单位长度,再向上平移3个单位长度 C、先向左平移2个单位长度,再向下平移3个单位长度 D、先向右平移2个单位长度,再向下平移3个单位长度9. 如图,等腰 中, ,AC与正方形DEFG的的边长DE在同一直线上, ,开始时点C与点D重合,让 沿直线DE向右平移,到点A与点E重合时停止.设CD的长为x , 与正方形DEFG重合部分的面积为y , 则能表示y与x之间关系的图象大致是( ). A、
A、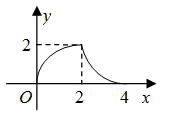 B、
B、 C、
C、 D、
D、 10. 二次函数 的图象如图所示,观察得出了下面4条信息:① ;② ;③ ;④ .你认为其中正确的结论有( )
10. 二次函数 的图象如图所示,观察得出了下面4条信息:① ;② ;③ ;④ .你认为其中正确的结论有( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 若 是二次函数,则 .12. 一元二次方程 的根是 .13. 已知 、 在抛物线 上,如果 ,那么 (填入“<”或“>”).14. 若m是方程 的一个根,则代数式 的值为.15. “新冠肺炎”防治取得战略性成果.若有一个人患了“新冠肺炎”,经过两轮传染后共有16个人患了“新冠肺炎”,则每轮传染中平均一个人传染了人.16. 如图, 是正方形 的中心, 是 内一点, ,将 绕 点旋转180°后得到 .若 , ,则 的长为.

三、解答题
-
17. 解方程 (用配方法、公式法两种方法求解)18. 已知抛物线的顶点为 ,且过点 .(1)、求抛物线的解析式;(2)、当 时,自变量 的取值范围是(直接写出结果).19. 如图,在平面直角坐标系中,已知点 , .
 (1)、画出将 绕原点逆时针旋转90°得到的 ;(2)、直接写出 的对应点 ( , ), 的对应点 ( , );(3)、若点 , 关于某点中心对称,则对称中心的坐标为.20. 已知一元二次方程 有两个根分别为 .(1)、求 的取值范围;(2)、若原方程的两个根 满足 ,求 的值.21. 如图,用一段长为 的篱笆围成一个一边靠墙的矩形菜园,墙长为 ,其中一边 留一道 宽的门.
(1)、画出将 绕原点逆时针旋转90°得到的 ;(2)、直接写出 的对应点 ( , ), 的对应点 ( , );(3)、若点 , 关于某点中心对称,则对称中心的坐标为.20. 已知一元二次方程 有两个根分别为 .(1)、求 的取值范围;(2)、若原方程的两个根 满足 ,求 的值.21. 如图,用一段长为 的篱笆围成一个一边靠墙的矩形菜园,墙长为 ,其中一边 留一道 宽的门. (1)、设图中 (与墙垂直的边)的长为 ,请用含 的式子表示 的长并直接写出 的取值范围;(2)、若整个菜园的总面积为 ,求 的长.22. 为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.(1)、李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)、设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?(3)、物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?23. 如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)、设图中 (与墙垂直的边)的长为 ,请用含 的式子表示 的长并直接写出 的取值范围;(2)、若整个菜园的总面积为 ,求 的长.22. 为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.(1)、李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)、设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?(3)、物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?23. 如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.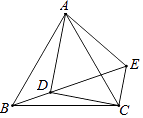 (1)、求证:AD=DE;(2)、求∠DCE的度数;(3)、若BD=1,求AD,CD的长.24. 如图,抛物线 经过点 ,与 轴交于 、 两点(点 在点 的左侧)与 轴交于点 .
(1)、求证:AD=DE;(2)、求∠DCE的度数;(3)、若BD=1,求AD,CD的长.24. 如图,抛物线 经过点 ,与 轴交于 、 两点(点 在点 的左侧)与 轴交于点 . (1)、求抛物线的解析式和 、 两点的坐标;(2)、已知点 在抛物线上,点 在该抛物线的对称轴上,
(1)、求抛物线的解析式和 、 两点的坐标;(2)、已知点 在抛物线上,点 在该抛物线的对称轴上,①当 时,求点 的坐标;
②是否存在这样的点 与点 ,使以 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.