湖北省十堰市丹江口市2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-30 类型:期中考试
一、单选题
-
1. 方程5x2-3x-2=0的二次项系数和一次项系数分别为( )A、5和3 B、5和-3 C、5和-2 D、5和22. 下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一元二次方程(a+1)x2-(a2-1)x+a2+a=0的一个根为0,则a的值为( )A、0 B、-1 C、0或-1 D、0或14. 对于抛物线 ,下列判断正确的是( )A、抛物线开口向上 B、抛物线的顶点是(-2,3) C、对称轴为直线x=2 D、它可由抛物线 向左平移2个单位再向上平移3个单位得到5. 用配方法解方程 时,方程可变形为( )A、 B、 C、 D、6. 若A(-2,y1),B(1,y2),C(2,y3)是抛物线 上的三个点,则y1 , y2 , y3的大小关系是( )A、y3>y2>y1 B、y1>y3>y2 C、y3>y1>y2 D、y1>y2>y37. 如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
3. 一元二次方程(a+1)x2-(a2-1)x+a2+a=0的一个根为0,则a的值为( )A、0 B、-1 C、0或-1 D、0或14. 对于抛物线 ,下列判断正确的是( )A、抛物线开口向上 B、抛物线的顶点是(-2,3) C、对称轴为直线x=2 D、它可由抛物线 向左平移2个单位再向上平移3个单位得到5. 用配方法解方程 时,方程可变形为( )A、 B、 C、 D、6. 若A(-2,y1),B(1,y2),C(2,y3)是抛物线 上的三个点,则y1 , y2 , y3的大小关系是( )A、y3>y2>y1 B、y1>y3>y2 C、y3>y1>y2 D、y1>y2>y37. 如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )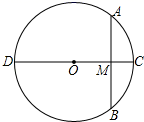 A、 cm B、8cm C、6cm D、4cm8. 新冠病毒主要是经呼吸道飞沫传播的,在无防护下传播速度很快,已知有1个人患了新冠,经过两轮传染后共有625个人患了新冠,每轮传染中平均一个人传染m人,则m的值为( )A、20 B、22 C、24 D、259. 函数y=kx2﹣4x+2的图象与x轴有公共点,则k的取值范围是( )A、k<2 B、k<2 且 k≠0 C、k≤2 D、k≤2 且 k≠010. 已知二次函数 (a<0)的图象过点(1,0)和(x1 , 0),且﹣2<x1<﹣1,下列4个判断中:①a+b=-1;②a>b﹣1;③b﹣a<0;④﹣1<a<﹣ ,正确的是( )A、①②③ B、①②④ C、①③④ D、②③④
A、 cm B、8cm C、6cm D、4cm8. 新冠病毒主要是经呼吸道飞沫传播的,在无防护下传播速度很快,已知有1个人患了新冠,经过两轮传染后共有625个人患了新冠,每轮传染中平均一个人传染m人,则m的值为( )A、20 B、22 C、24 D、259. 函数y=kx2﹣4x+2的图象与x轴有公共点,则k的取值范围是( )A、k<2 B、k<2 且 k≠0 C、k≤2 D、k≤2 且 k≠010. 已知二次函数 (a<0)的图象过点(1,0)和(x1 , 0),且﹣2<x1<﹣1,下列4个判断中:①a+b=-1;②a>b﹣1;③b﹣a<0;④﹣1<a<﹣ ,正确的是( )A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
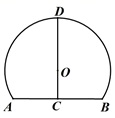
11. 一元二次方程x2﹣x=0的根是 .12. 抛物线 经过点A(-3,0),B(1,0)两点,则关于x的一元二次方程 的解是.13. 抛物线 交y轴于点M,点M关于其对称轴的对称点N的坐标为.14. 如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果C是⊙O中弦AB的中点,CD经过圆心O交⊙O于点D,并且AB=8m,CD=8m,则⊙O的半径长为cm.
 15. 如图,等腰直角△ABC中,AC=BC=6,∠ACB=90°,点O是斜边AB上一点,将△BOC绕C点顺时针方向旋转到△AQC的位置,连接OQ,OQ的最小值为.
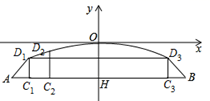
15. 如图,等腰直角△ABC中,AC=BC=6,∠ACB=90°,点O是斜边AB上一点,将△BOC绕C点顺时针方向旋转到△AQC的位置,连接OQ,OQ的最小值为.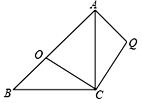 16. 如图,一个拱形桥架可以近似看作是由等腰梯形ABD3D1和其上方的抛物线D1OD3组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-14,-1.96),则桥架的拱高OH=米.
16. 如图,一个拱形桥架可以近似看作是由等腰梯形ABD3D1和其上方的抛物线D1OD3组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-14,-1.96),则桥架的拱高OH=米.
三、解答题
-
17. 解方程: .18. 已知二次函数图象的顶点坐标是(1,-4),且与y轴交于点(0,-3),求此二次函数的解析式19. 如图,四边形ABCD是边长为4的正方形,且DE=1,△ABF是△ADE的旋转图形.
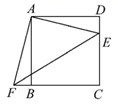 (1)、求AF的长;(2)、求△AEF的面积.20. 如图,A,B是⊙O上两点,∠AOB=120°,C为弧AB上一点.
(1)、求AF的长;(2)、求△AEF的面积.20. 如图,A,B是⊙O上两点,∠AOB=120°,C为弧AB上一点.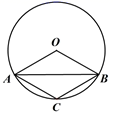 (1)、求∠ACB的度数;(2)、若C是弧AB的中点,求证:四边形OACB是菱形.21. 已知关于x的一元二次方程 有两个不相等的实数根.(1)、求实数k的取值范围;(2)、若方程的两根x1、x2满足 ,求k的值.22. 如图,要为一幅长30cm、宽20cm的照片配一个镜框,要求镜框四边的宽度x相等,且镜框所占面积为照片面积的 ,镜框的宽度应该多少厘米?
(1)、求∠ACB的度数;(2)、若C是弧AB的中点,求证:四边形OACB是菱形.21. 已知关于x的一元二次方程 有两个不相等的实数根.(1)、求实数k的取值范围;(2)、若方程的两根x1、x2满足 ,求k的值.22. 如图,要为一幅长30cm、宽20cm的照片配一个镜框,要求镜框四边的宽度x相等,且镜框所占面积为照片面积的 ,镜框的宽度应该多少厘米? 23. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.
23. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.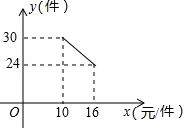 (1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?24. 正方形ABCD的四个顶点都在⊙O上,E是⊙O上的一点.
(1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?24. 正方形ABCD的四个顶点都在⊙O上,E是⊙O上的一点.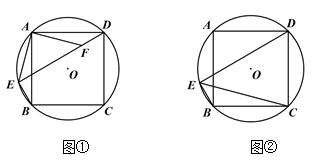 (1)、如图①,若点E在 上,F是DE上的一点,DF=BE.求证:△ADF≌△ABE;(2)、在(1)的条件下,小明还发现线段DE、BE、AE之间满足等量关系:DE-BE= AE.请说明理由;(3)、如图②,若点E在 上.连接DE,CE,已知BC=5,BE=1,求DE及CE的长.25. 如图①,在平面直角坐标系中,已知抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)、如图①,若点E在 上,F是DE上的一点,DF=BE.求证:△ADF≌△ABE;(2)、在(1)的条件下,小明还发现线段DE、BE、AE之间满足等量关系:DE-BE= AE.请说明理由;(3)、如图②,若点E在 上.连接DE,CE,已知BC=5,BE=1,求DE及CE的长.25. 如图①,在平面直角坐标系中,已知抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.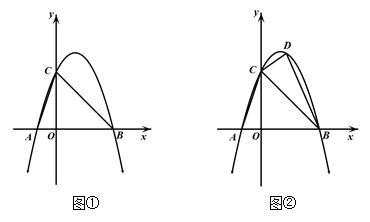 (1)、求该抛物线的解析式;(2)、如图②,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,当△BCD的面积等于△AOC面积的2倍时,求m的值;(3)、抛物线上是否存在点P,使∠CBP+∠ACO=∠ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、如图②,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,当△BCD的面积等于△AOC面积的2倍时,求m的值;(3)、抛物线上是否存在点P,使∠CBP+∠ACO=∠ABC?若存在,请求出点P的坐标;若不存在,请说明理由.