湖北省恩施土家族苗族自治州巴东县2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-30 类型:期中考试
一、单选题
-
1. 一元二次方程 的解是( )A、-1 B、1 C、0 D、±12. 二次函数y=x2﹣2x+2的顶点坐标是( )A、(1,1) B、(2,2) C、(1,2) D、(1,3)3. 下列图形是中心对称图形的有( )个.
①平行四边形:②等边三角形;③线段;④角
A、1 B、2 C、3 D、44. 二次函数 的图象的对称轴是( )A、 B、 C、 或 D、5. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、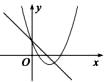 B、
B、 C、
C、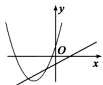 D、
D、 6. 已知二次函数 ,则 的值为( )A、-3 B、±3 C、3 D、7. 以原点为中心,把点 逆时针旋转270°,得到点 ,则点 的坐标为( )A、 B、 C、 D、8. 如图是 的小方格构成的正方形 ,若将其中的两个小方格涂黑,使得涂黑后的整个 图案(含阴影)既是轴对称图形,又是中心对称图形,则这样的图案有( )种.
6. 已知二次函数 ,则 的值为( )A、-3 B、±3 C、3 D、7. 以原点为中心,把点 逆时针旋转270°,得到点 ,则点 的坐标为( )A、 B、 C、 D、8. 如图是 的小方格构成的正方形 ,若将其中的两个小方格涂黑,使得涂黑后的整个 图案(含阴影)既是轴对称图形,又是中心对称图形,则这样的图案有( )种.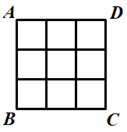 A、8 B、6 C、4 D、29. 已知 , , 分别是三角形的三边长,则关于 的方程 根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有且只有一个实数根 D、没有实数根10. 已知二次函数 ( , , , 为常数),根据下表所列 与 的几组对应值,则方程 一个根的范围是( )
A、8 B、6 C、4 D、29. 已知 , , 分别是三角形的三边长,则关于 的方程 根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有且只有一个实数根 D、没有实数根10. 已知二次函数 ( , , , 为常数),根据下表所列 与 的几组对应值,则方程 一个根的范围是( )3.23
3.24
3.25
3.26
0.03
0.09
A、 B、 C、 D、11. 如图,将等边 绕点 逆时针旋转得到 ,旋转角为 .若 ,则 的大小是( )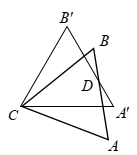 A、20° B、40° C、60° D、80°12. 已知二次函数 的图象如图所示,下列结论:
A、20° B、40° C、60° D、80°12. 已知二次函数 的图象如图所示,下列结论:① ;② ;③方程 有两个相等的实数根;④方程 的两根是 ,
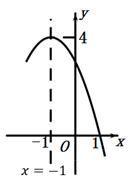
其中正确的结论有( )个.
A、1 B、2 C、3 D、4二、填空题
-
13. 一元二次方程 化成一般形式.14. 在直角坐标系中,已知 , ,则点 关于点 的对称点 的坐标为.15. 把抛物线 向下平移1个单位长度,再向左平移1个单位长度,得到的抛物线解析式是.16. 东宇村种植的椪柑2017年每亩收 ,2019年每亩收 ,则椪柑每亩产量的年平均增长率为.
三、解答题
-
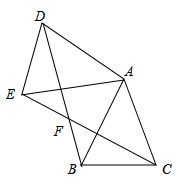
17.(1)、用公式法解方程: .(2)、用配方法解方程: .18. 如图,四边形 的两条对线 、 互相垂直, ,设 , .
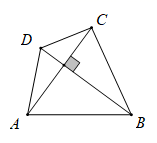
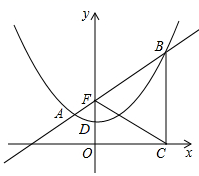
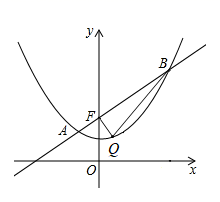
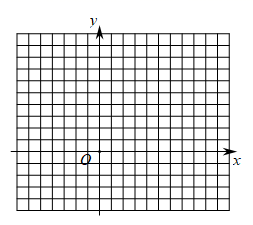 (1)、求 与 的函数关系式.(2)、画出函数图象.19. 如图,在等腰直角三角形 中, , ,点 为边 上任意一点,点 为 的中点,过点 作 交 于点 .求证: 为定值.
(1)、求 与 的函数关系式.(2)、画出函数图象.19. 如图,在等腰直角三角形 中, , ,点 为边 上任意一点,点 为 的中点,过点 作 交 于点 .求证: 为定值.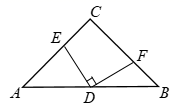 20. 要设计长 、宽 的图案,其中有两横、两纵的彩条(图中阴影部分),已知横竖彩条的宽度比为 ,如果要使彩条所占面积是整个图案面积的 ,求横纵彩条的宽度.
20. 要设计长 、宽 的图案,其中有两横、两纵的彩条(图中阴影部分),已知横竖彩条的宽度比为 ,如果要使彩条所占面积是整个图案面积的 ,求横纵彩条的宽度.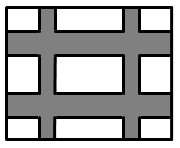 21. 已知关于 的一元二次方程 .(1)、求证:无论 取何实数,原方程总有两个实数根.(2)、设方程的两实数根为 、 ,若 ,求 的值.22. 如图,在 中, , , ,点 从点 开始沿 边向点 以 的速度运动;点 从点 开始沿 边向点 以 的速度运动,如果 , 分别从 , 同时出发,当其中一个点到达终点时另一个点也随之停止运动,设 的面积为 ,点 , 的运动时间为 .
21. 已知关于 的一元二次方程 .(1)、求证:无论 取何实数,原方程总有两个实数根.(2)、设方程的两实数根为 、 ,若 ,求 的值.22. 如图,在 中, , , ,点 从点 开始沿 边向点 以 的速度运动;点 从点 开始沿 边向点 以 的速度运动,如果 , 分别从 , 同时出发,当其中一个点到达终点时另一个点也随之停止运动,设 的面积为 ,点 , 的运动时间为 .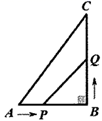 (1)、经过几秒后, 的长度等于 ?(2)、 的面积 随时间 如何变化?写出 与 的函数解析式及 的取值范围.
(1)、经过几秒后, 的长度等于 ?(2)、 的面积 随时间 如何变化?写出 与 的函数解析式及 的取值范围.