湖北省鄂州市鄂城区2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-30 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列四个图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线 $y = - 2 {(x + 2)}^{2} - 3$ 的顶点坐标是（）

A、（2，-3） B、（-2，-3） C、（-2，3） D、（2，3）

查看试题解析
3. 用配方法解方程 $x^{2} + 2 x - 5 = 0$ 时，原方程应变形为（）

A、 ${(x - 1)}^{2} = 6$ B、 ${(x + 1)}^{2} = 3$ C、 ${(x - 1)}^{2} = 3$ D、 ${(x + 1)}^{2} = 6$

查看试题解析
4. 一个等腰三角形的两条边长分别是方程 $x^{2} - 7 x + 10 = 0$ 的两根，则该等腰三角形的周长是（）

A、12 B、9 C、13 D、12或9

查看试题解析
5. 将抛物线 $y = x^{2}$ 向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的函数表达式为（）

A、 $y = {(x + 2)}^{2} - 3$ B、 $y = {(x + 2)}^{2} + 3$ C、 $y = {(x - 2)}^{2} + 3$ D、 $y = {(x - 2)}^{2} - 3$

查看试题解析
6. 已知抛物线y＝ $x^{2}$ ﹣x﹣1与x轴的一个交点为(m，0)，则代数式m²﹣m+2019的值为（）

A、2018 B、2019 C、2020 D、2021

查看试题解析
7. 如图，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（）

A、35° B、40° C、50° D、65°

查看试题解析
8. 要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛.设比赛组织者应邀请x个队参赛，则x满足的关系式为（）

A、 $\frac{1}{2} x (x + 1) = 4 \times 7$ B、 $\frac{1}{2} x (x - 1) = 4 \times 7$ C、x（x+1）＝28 D、x（x﹣1）＝28

查看试题解析
9. 如图，开口向下的抛物线 $y = a x^{2} + b x + c$ 交y轴正半轴于点A，对称轴为直线x=1.下列结论：① $b = - 2 a$ ；②若抛物线经过点（ -1，0），则 $9 a + 3 b + c = 0$ ；③ $a b c > 0$ ； $④$ 若（ $x_{1}$ ， $y_{1}$ ），（ $x_{2}$ ， $y_{2}$ ）是抛物线上两点，且 $x_{1} < x_{2}$ ，则 $y_{1} < y_{2}$ . 其中正确的结论是（）

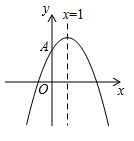A、①④ B、①② C、③④ D、②③

查看试题解析
10. 关于x的函数y=ax²+(2a+1)x+a-1与坐标轴有两个交点，则a的取值有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

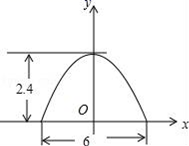
11. 在平面直角坐标系中，点A（-2，-4）关于原点对称的点 $A^{'}$ 的坐标是.

查看试题解析
12. 当方程 $(m - 1) x^{m^{2} + 1} - (m + 1) x - 2 = 0$ 是关于x一元二次方程时， $m$ 的值；

查看试题解析
13. 已知 $α$ ， $β$ $是$ 方程 $x^{2} + 2 x - 5 = 0$ 的两根，那么 $α^{2} + α β + 3 α + β$ 的值是.

查看试题解析
14. 已知抛物线y＝x²+mx+9的顶点在x轴上，则m的值为.

查看试题解析
15. 某菜农搭建了一个横截面为抛物线的大棚，尺寸如图，若菜农身高为1.8m，他在不弯腰的情况下，在棚内的横向活动范围是m.

查看试题解析
16. 已知实数m，n满足条件 $m^{2} - 7 m + 2 = 0$ ， $n^{2} - 7 n + 2 = 0$ ，则 $\frac{n}{m} + \frac{m}{n}$ 的值是.

查看试题解析

三、解答题

17. 用合适的方法解下列方程：

(1)、 $x^{2} - 4 x - 7 = 0$ ；

(2)、 $x^{2} - 4 x - 12 = 0$ ；

(3)、 ${(2 x - 3)}^{2} = 5 (2 x - 3)$ .

查看试题解析
18. 在平面直角坐标系中，△ABC的位置如图所示 $（$ 每个小方格都是边长为1个单位长度的正方形 $）$ .

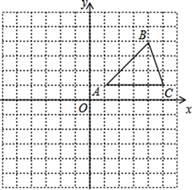
（ 1 ）将△ABC绕着点A顺时针旋转 $90 °$ ，画出旋转后得到的△AB₁C₁；直接写出点B₁的坐标；

（ 2 ）作出△ABC关于原点O成中心对称的△A₂B₂C₂ ，并直接写出点B₂的坐标.

查看试题解析
19. 关于 $x$ 的一元二次方程 $x^{2} + (2 k + 1) x + k^{2} + 1 = 0$ 有两个不等实根 $x_{1}$ ， $x_{2}$ .

(1)、求实数 $k$ 的取值范围；

(2)、若方程两实根 $x_{1}$ ， $x_{2}$ 满足 $x_{1} + x_{2} = - x_{1} \cdot x_{2}$ ，求 $k$ 的值。

查看试题解析
20. 如图，二次函数 $y_{1} = - \frac{2}{5} x^{2} + b x + c$ 的图象与x轴、y轴分别交于点A（-1，0）和点B（0，2），图象的对称轴交x轴于点C，一次函数 $y_{2} = m x + n$ 的图象经过点B，C，与二次函数图象的另一个交点为点D.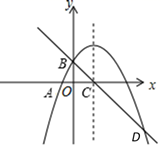

(1)、求二次函数的解析式 $y_{1}$ 和一次函数的解析式 $y_{2}$ ；

(2)、求点D的坐标；

(3)、结合图象，请直接写出 $y_{1} \leq y_{2}$ 时，x的取值范围：.

查看试题解析
21. 如图，利用一面墙（墙长10米）用20米的篱笆围成一个矩形场地.设垂直于墙的一边为x米，矩形场地的面积为S平方米.

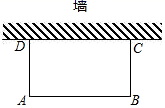(1)、求S与x的函数关系式，并求出x的取值范围；

(2)、若矩形场地的面积为48平方米，求矩形场地的长与宽.

查看试题解析
22. 如图，点O是等边三角形ABC内一点，∠AOB=110°，∠BOC=β．将△BOC绕点C按顺时针方向旋转60°得到△ADC，连接OD．

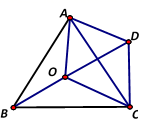(1)、求证：△COD是等边三角形；

(2)、当β=150°时，试判断△AOD的形状，并说明理由；

(3)、探究：当β为多少度时，△AOD是以OD为底边的等腰三角形？

查看试题解析
23. 某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．

(1)、求y与x之间的函数关系式；

(2)、当每件售价定为多少元时，每星期的销售利润最大，最大利润是多少元？

(3)、若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？

查看试题解析
24. 如图，抛物线y=ax²+2x﹣3a经过A（1，0）、B（b，0）、C（0，c）三点.

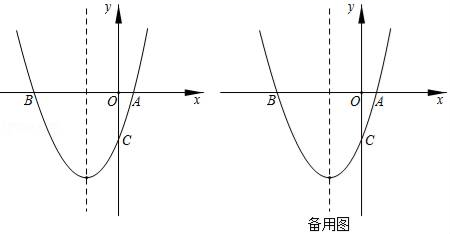(1)、求b，c的值；

(2)、在抛物对称轴上找一点P，使PA+PC的值最小，求点P的坐标；

(3)、点M为x轴上一动点，抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由.

查看试题解析