湖北省宜昌市五峰土家族自治县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-30 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）
    A、 B、 C、 D、

    查看试题解析

  • 2. 如果两个图形全等，则这个图形必定是（   ）
    A、形状相同，但大小不同 B、形状大小均相同 C、大小相同，但形状不同 D、形状大小均不相同

    查看试题解析

  • 3. 在△ABC中，已知已知△ABC的三个内角之比为1：2：3，则这个三角形的形状为（   ）
    A、锐角三角形 B、钝角三角形 C、直角三角形 D、等腰三角形

    查看试题解析

  • 4. 如图，在△ABC中，AB边上的高是（   ）.

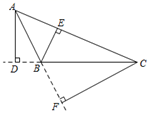    A、AD B、BE C、CF D、BF

    查看试题解析

  • 5. 下列哪组数据能构成三角形的三边（  ）
    A、1cm、2cm、3cm B、2cm、3cm、4cm C、14cm、4cm、9cm D、7cm、2cm、4cm

    查看试题解析

  • 6. 如图，已知△ABC中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（   ）

     

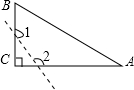    A、90° B、135° C、270° D、315°

    查看试题解析

  • 7. 如图，在△ABC中，∠A=50°，∠1=30°，∠2=40°，∠D的度数是（ ）

    A、110° B、120° C、130° D、140°

    查看试题解析

  • 8. 如图，在下列条件中，不能证明△ABC≌△DCB的是（   ）.

    A、AB=DC ， AC=DB B、AB=DC ， ∠ABC=∠DCB C、∠ACB=∠DBC， ∠A=∠D D、AC=BD ， ∠A=∠D

    查看试题解析

  • 9. 花花不慎将一块三角形的玻璃打碎成了如图所示的四块（图中所标①、②、③、④），若要配一块与原来大小一样的三角形玻璃，应该带（   ）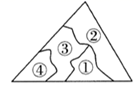

    A、第①块 B、第②块 C、第③块 D、第④块

    查看试题解析

  • 10. 李老师用直尺和圆规作已知角的平分线．

    作法：①以点O为圆心，适当长为半径画弧，交OA于点D，交OB于点E

    ②分别以点D、E为圆心，大于 12 DE的长为半径画弧，两弧在∠AOB的内部相交于点C．

    ③画射线OC，则OC就是∠AOB的平分线．

    李老师用尺规作角平分线时，用到的三角形全等的判定方法是（   ）

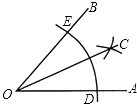    A、SSS B、SAS C、ASA D、AAS

    查看试题解析

  • 11. 六盘水市“琼都大剧院”即将完工，现需选用同一批地砖进行装修，以下不能镶嵌的地板是（　　）

    A、正五边形地砖 B、正三角形地砖 C、正六边形地砖 D、正四边形地砖

    查看试题解析

二、填空题

  • 12. 一个n边形的内角和是540°，那么n= ．

    查看试题解析

  • 13. 如图，小亮从A点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，……照这样走下去，他第一次回到出发地A点时，一共走了米.

    查看试题解析

  • 14. 空调安装在墙上时，一般会用如图所示的三角形支架固定在墙上，这种方法应用的数学知识是.

    查看试题解析

  • 15. 如图， △ABC 中， AD⊥BC 于D，要使 △ABD≌△ACD ，若根据“ HL ”判定，还需要加条件

    查看试题解析

三、解答题

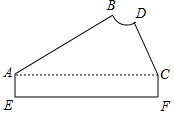
  • 16. 如图，按规定，一块横板中AB、CD的延长线相交成85°角，因交点不在板上，不便测量，工人师傅连接AC，测得∠BAC=32°，∠DCA=65°，此时AB、CD的延长线相交所成的角是不是符合规定？为什么？

    查看试题解析

  • 17. 如图，有一座锥形小山，要测量锥形小山两端A、B的距离，先在平地上取一个可以直接到达A和B的点C，连接AC并延长到点D，使CD=CA，连接BC并延长到点E，使CE=CB，连接DE，那么量出DE的长，就是A、B的距离.你能说说其中的道理吗？

    查看试题解析

  • 18. 如图，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1+∠2=90°．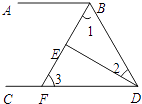

    (1)、试说明：AB∥CD； 
    (2)、若∠2=25°，求∠3的度数．

    查看试题解析

  • 19. 如图，点A、D、C、F在同一条直线上，AD=CF，AB=DE，BC=EF.

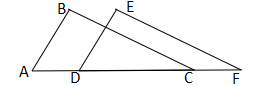    (1)、求证：ΔABC≌△DEF；
    (2)、若∠A=55°，∠B=88°，求∠F的度数.

    查看试题解析

  • 20. 已知：如图， MS⊥PS ， MN⊥SN ， PQ⊥SN ，垂足分别是S，N，Q，且 MS=PS .

    (1)、求证：△MNS≌△SQP；
    (2)、如果 PQ=6 ， MN=4 ，求NQ的长.

    查看试题解析

  • 21. 已知：如图，在△ABC中，AD是BC边上的高，AE是∠BAC平分线，∠B=30°，∠DAE=15°，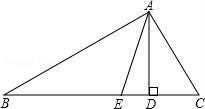

    (1)、求∠BAE的度数；
    (2)、求∠C的度数．

    查看试题解析

  • 22. 如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF，

    (1)、求证：AD平分∠BAC；
    (2)、已知AC=20， BE=4，求AB的长.

    查看试题解析

  • 23. 如图，在△ABC中，∠ACB＝90°，AC＝7cm，BC＝3cm，CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动，过点E作BC的垂线交直线CD于点F.

    (1)、试说明：∠A＝∠BCD；
    (2)、当点E运动多长时间时，CF＝AB.请说明理由.

    查看试题解析

  • 24. 如图

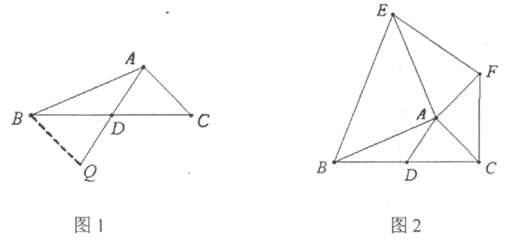    (1)、阅读理解：课外兴趣小组活动时，老师提出了如下问题：

    在△ABC中，AB＝9，AC＝5，求BC边上的中线AD的取值范围.

    小明在组内经过合作交流，得到了如下的解决方法（如图1）：

    ①延长AD到Q，使得DQ＝AD；

    ②再连接BQ，把AB、AC、2AD集中在△ABQ中；

    ③利用三角形的三边关系可得4<AQ<14，则AD的取值范围是 .

    感悟：解题时，条件中若出现“中点”“中线”等条件，可以考虑倍长中线，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中.

    (2)、请你写出图1中AC与BQ的位置关系并证明.
    (3)、思考：已知，如图2，AD是△ABC的中线，AB＝AE，AC＝AF，∠BAE＝∠FAC＝90°.试探究线段AD与EF的数量和位置关系并加以证明.

    查看试题解析