湖北省襄阳市襄城区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-09-30 类型:期中考试
一、单选题
-
1. 下列大学的校徽图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列各组线段为边,能组成三角形的是 ( )A、1cm,3cm,5cm B、2cm,2cm,6cm C、3cm,4cm,5cm D、4cm,6cm,10cm3. 下列设备,没有利用三角形稳定性的是( )A、自行车的三角形车架 B、伸缩门 C、屋顶三角形钢架 D、起重机4. 画△ABC中BC边上的高,下列四个画法中正确的是( )A、
2. 以下列各组线段为边,能组成三角形的是 ( )A、1cm,3cm,5cm B、2cm,2cm,6cm C、3cm,4cm,5cm D、4cm,6cm,10cm3. 下列设备,没有利用三角形稳定性的是( )A、自行车的三角形车架 B、伸缩门 C、屋顶三角形钢架 D、起重机4. 画△ABC中BC边上的高,下列四个画法中正确的是( )A、 B、
B、 C、
C、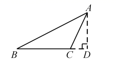 D、
D、 5. 如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
5. 如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( ) A、AAS B、ASA C、SAS D、SSS6. 内角和为540°的多边形是( )A、
A、AAS B、ASA C、SAS D、SSS6. 内角和为540°的多边形是( )A、 B、
B、 C、
C、 D、
D、 7. 等腰三角形的周长为13 cm,其中一边长为3 cm,则该等腰三角形的底边长为( )A、3cm B、5cm C、7cm或3cm D、8cm8. 如图所示,AB=CD , ∠ABD=∠CDB , 则图中全等三角形共有( )
7. 等腰三角形的周长为13 cm,其中一边长为3 cm,则该等腰三角形的底边长为( )A、3cm B、5cm C、7cm或3cm D、8cm8. 如图所示,AB=CD , ∠ABD=∠CDB , 则图中全等三角形共有( ) A、5对 B、4对 C、3对 D、2对9.
A、5对 B、4对 C、3对 D、2对9.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于( )
 A、60° B、50° C、45° D、30°10. 如图,△ABD与△ACE都是等边三角形,AB≠AC,下列四个结论,①BE=CD;②∠BOD=60°;③∠BDO=∠CEO;④若∠BAC=90°,且DA∥BC,则BC⊥CE.其中正确的个数有( )
A、60° B、50° C、45° D、30°10. 如图,△ABD与△ACE都是等边三角形,AB≠AC,下列四个结论,①BE=CD;②∠BOD=60°;③∠BDO=∠CEO;④若∠BAC=90°,且DA∥BC,则BC⊥CE.其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若等腰三角形的一个底角为40°,则它的顶角为度.12. 如图, ,要使 ,还需添加一个条件是:.(填上你认为适当的一个条件即可)
 13. 如图,△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积.
13. 如图,△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积.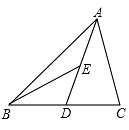 14. 如图,∠AOC=∠BOC=15°,CF∥OA,CE⊥OA于点E,若CF=16,则CE=.
14. 如图,∠AOC=∠BOC=15°,CF∥OA,CE⊥OA于点E,若CF=16,则CE=. 15. 如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE=°.
15. 如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE=°. 16. 如图,已知P(3,3),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=.
16. 如图,已知P(3,3),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=.
三、解答题
-
17. 在△ABC中,∠A=∠B+10°,∠C=∠B-40°,求△ABC的各个内角的度数.18. 如图,已知点B,C,F,E在同一直线上,∠1=∠2,BC=EF,AB∥DE.求证:AC=DF.
 19. 如图是由36个边长为1的小正方形拼成的网格图,请按照要求画图:
19. 如图是由36个边长为1的小正方形拼成的网格图,请按照要求画图: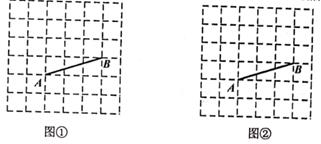 (1)、在图①中画出2个以AB为腰且底边不等的等腰△ABC,要求顶点C是格点;(2)、在图②中画出1个以AB为底边的等腰△ABC,要求顶点C是格点。20. 如图所示:
(1)、在图①中画出2个以AB为腰且底边不等的等腰△ABC,要求顶点C是格点;(2)、在图②中画出1个以AB为底边的等腰△ABC,要求顶点C是格点。20. 如图所示:
( 1 )作出△ABC关于x轴对称的 ,并写出 三个顶点的坐标.
( 2 )在y轴上画出点P,使PA+PC的值最小.
21. 如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上.若∠B=60°,求证:CE=AC+CD. 22. 如图,∠B=∠C=90°,E是BC的中点,AE平分∠BAD,求证:AE⊥DE.
22. 如图,∠B=∠C=90°,E是BC的中点,AE平分∠BAD,求证:AE⊥DE.

