湖北省武汉市硚口区、经开区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2021-09-30 类型：期中考试
一、单选题
-
1. 大自然中存在很多对称现象，下列植物叶子的图案中不是轴对称图形的是（ ）
A、
B、
C、
D、
2. 下列长度的三条线段，能组成三角形的是（ ）A、3，4，8 B、5，6，10 C、5，5，11 D、5，6，113. 下列命题，真命题是（ ）A、全等三角形的面积相等 B、面积相等的两个三角形全等 C、两个角对应相等的两个三角形全等 D、两边和其中一边的对角对应相等的两个三角形全等4. 如图，在△ABC和△DEF中，AB＝DE，AB DE，运用“SAS”判定△ABC≌△DEF，需补充的条件是（ ）
A、AC＝DF B、∠A＝∠D C、BE＝CF D、∠ACB＝∠DFE5. 在平面直角坐标系中，点P（﹣3，4）关于y轴的对称点的坐标为（ ）A、（4，﹣3） B、（3，﹣4） C、（3，4） D、（﹣3，﹣4）6. 用一批完全相同的正多边形能镶嵌成一个平面图案的是（ ）A、正五边形 B、正六边形 C、正七边形 D、正八边形7. 若一个多边形的每个内角都等于150°，则这个多边形的边数是（ ）A、10 B、11 C、12 D、138. 如图，在△ABC中，AD⊥BC，垂足为D，EF垂直平分AC，交AC于点F，交BC于点E，BD＝DE，若△ABC的周长为26cm，AF＝5cm，则DC的长为（ ）
A、8cm B、7cm C、10cm D、9cm9. 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和38，则△EDF的面积为（ ）
A、6 B、12 C、4 D、810. 如图，点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点（其中P，Q不与端点重合），点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，连接AQ、CP交于点M，下列结论：①AQ＝CP；②∠CMQ的度数等于60°；③当△PBQ为直角三角形时，t＝ 秒.其中正确的结论有（ ）
A、0个 B、1个 C、2个 D、3个二、填空题
-
11. 工人师傅在做完门框后，为防止变形，经常如图所示钉上两根斜拉的木条（即图中的AB、CD两根木条），这样做的数学原理是：.
12. 从一个多边形的一个顶点出发一共有7条对角线，则这个多边形的边数为 ．13. 等腰三角形的周长为16cm，一边长为4cm，则腰长为cm.14. 如图，线段AB、BC的垂直平分线l1、l2相交于点O，若∠1＝39°，则∠AOC＝.
15. 如图，在等腰△ABC中，AB＝AC，BD是平分线，若BD＝BC，则∠A的度数为.
16. 如图，在Rt△ABC中，∠A＝90°，∠B＝60°，BC＝4，若E是BC上的动点，F是AC上的动点，则AE+EF的最小值为.
三、解答题
-
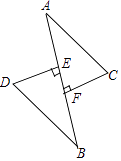
17. 一个多边形的内角和比它的外角和多720°，求该多边形的边数.18. 如图，DE⊥AB，CF⊥AB，垂足分别是点E、F，DE=CF，AE=BF，求证：AC∥BD．
19. 如图，在Rt△ABC中，∠C＝90°，BD平分∠ABC交AC于点D，AP平分∠BAC交BD于点P，∠BDC＝58°，求∠BAP的度数.
20. 如图，在等腰Rt△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF.
(1)、求证：BE＝BF；(2)、连接EF，求证：∠CFE＝∠CAE.21. 如图
(1)、如图1，在平面直角坐标系中，A（2，﹣1），B（4，2），C（1，4）.①画出△ABC关于y轴对称的△A1B1C1 ， 并写出点A1的坐标；
②判断△ABC的形状，并写出△ABC的面积；
③请仅用无刻度的直尺画出∠ABC的平分线BD（保留画图痕迹）.
(2)、如图2是4×4的正方形网格，请仅用无刻度的直尺在直线l上画出一条1个单位长度的线段MN（M在N的上方），使AM+NB的值最小（保留画图痕迹）.22. 已知在等腰Rt△ABC中，∠BAC＝90°，AB＝AC.
(1)、如图1，若△ADE是等腰直角三角形，∠DAE＝90°，AD＝AE，连接BE，CD.求证：BE⊥CD；(2)、如图2，若O是BC的中点，M，N分别在AB，AC上，OM⊥ON.求证：AM＝CN；(3)、如图3，在（1）的基础上，G是EC的中点，连接GB并延长至点F，CF＝CD.求证：∠EBG＝∠BFC.23. 如图
(1)、如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF＝BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系.小王同学探究此问题的方法是：延长FD到点G，使DG＝BE.连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ▲ ；(2)、如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°.E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；(3)、如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程.24. 在平面直角坐标系中，点A在y轴正半轴上，点B在x轴负半轴上，BP平分∠ABO.
(1)、如图1，点T在BA延长线上，若AP平分∠TAO，求∠P的度数；(2)、如图2，点C为x轴正半轴上一点，∠ABC＝2∠ACB，且P在AC的垂直平分线上.①求证：AP BC；
②D是AB上一点，E是x轴正半轴上一点，连接AE交DP于H.当∠DHE与∠ABE满足什么数量关系时，DP＝AE.给出结论并说明理由.