湖北省武汉市汉阳区2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-30 类型：期中考试

进入出卷网下载

一、单选题

1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 计算 $\sqrt{16}$ 的结果是（）

A、±4 B、±8 C、4 D、2

查看试题解析
3. 给出下列长度的三条线段，能组成三角形的是（）

A、3，4，5 B、8，6，15 C、13，12，25 D、7，2，3

查看试题解析
4. 三角形具有稳定性，所以要使如图所示的五边形木架不变形，至少要使钉上（）根木条

A、1 B、2 C、3 D、4

查看试题解析
5. 用直尺和圆规作两个全等三角形，如图，能得到 $△ C O D ≅ △ C' O' D'$ 的依据是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析
6. 如图，在△ABC中，D是BC边上一点，且AB＝AD＝DC ， ∠BAD＝40°，则∠C为（）

A、25° B、35° C、40° D、50°

查看试题解析
7. 如图，在 $△ A B C$ 中，点 $D$ 在 $B C$ 边上，将点 $D$ 分别以 $A B$ ， $A C$ 为对称轴，画出对称点 $E$ ， $F$ ，并连接 $A E$ ， $A F$ .根据图中标示的角度，可得 $∠ E A F$ 的大小为（）

A、 $108 °$ B、 $115 °$ C、 $122 °$ D、 $130 °$

查看试题解析
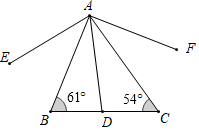8.
如图，△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于点D，DE⊥AB，垂足为E，且AB=6cm，则△DEB的周长为（　　）

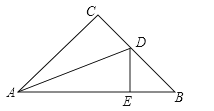A、4cm B、6cm C、8cm D、10cm

查看试题解析
9. 如图， $Δ A B C ， Δ E C D$ 都是等边三角形，且B，C，D在一条直线上，连结 $B E ， A D$ ，点M，N分别是线段BE，AD上的两点，且 $B M = \frac{1}{3} B E ， A N = \frac{1}{3} A D$ ，则 $Δ C M N$ 的形状是（）

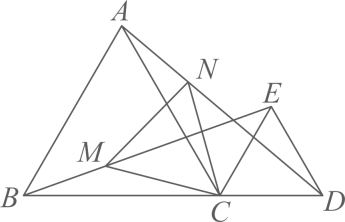A、等腰三角形 B、直角三角形 C、等边三角形 D、不等边三角形

查看试题解析
10. 如图，方格中 $△ A B C$ 的三个顶点分别在小正方形的顶点（格点上），这样的三角形叫做格点三角形，图中可以画出与 $△ A B C$ 全等的格点三角形（不含 $△ A B C$ ）共有（）

A、21个 B、22个 C、23个 D、39个

查看试题解析

二、填空题

11. 已知点P关于x轴的对称点P1的坐标是（2，1），则点P的坐标是．

查看试题解析
12. 如图中的两个三角形全等，图中的字母 $a$ ， $b$ ， $c$ 表示三角形的边长，则 $∠ 1$ 的大小是.

查看试题解析
13. 一个多边形的内角和是它的外角和的4倍，则这个多边形的边数是．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点 $A$ 的坐标为 $(- 7 ， 3)$ ，点 $C$ 的坐标为 $(- 2 ， 0)$ ，则点 $B$ 的坐标是.

查看试题解析
15. 如图， $B D$ 为 $△ A B C$ 的角平分线，且 $B D = B C$ ， $E$ 为 $B D$ 延长线上一点， $B E = B A$ ，过 $E$ 作 $E F ⊥ A B$ 于 $F$ ，下列结论：
① $∠ B C E + ∠ B D C = 180 °$ ；② $A D = A E = E C$ ；③ $A B / / C E$ ；④ $B A + B C = 2 B F$ .

其中正确的序号是.

查看试题解析
16. 如图，在四边形 ABCD 中，AC 是对角线，AB=CD，∠DAC+∠BCA=180°，∠BAC+∠ACD=90°，四边形 ABCD 的面积是 18，则 CD 的长是.

查看试题解析

三、解答题

17. 解方程组及不等式组.

(1)、 ${\begin{array}{l} 3 x - y = 5 \\ 5 x + 2 y = 12 \end{array}$

(2)、 ${\begin{array}{l} 2 x + 3 \geq x + 2 \\ \frac{2 x + 5}{3} - 1 < 2 - x \end{array}$

查看试题解析
18. 用一条长为 $18 cm$ 的细绳围成一个等腰三角形.

(1)、如果腰长是底边长的2倍，那么各边的长是多少？

(2)、能围成有一边长是 $4 cm$ 的等腰三角形吗？为什么？

查看试题解析
19. 如图，已知 $A C / / D F$ ， $∠ A = ∠ D$ ， $B E = C F$ .
求证： $△ A B C ≅ △ D E F$ .

查看试题解析
20. 在平面直角坐标系的网格中，横、纵坐标均为整数的点叫做格点，例如： $A (1 ， 1)$ ， $B (5 ， 1)$ ， $C (4 ， 4)$ ， $D (2 ， 3)$ 都是格点.用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由.

(1)、在图1中画出 $△ C A E ≅ △ A C B$ （其中点 $A$ 的对应点为点 $C$ ）；

(2)、在图2中画出 $A F$ ，使 $A F ⊥ B C$ ；

(3)、如图3，在线段 $A B$ 上画点 $G$ ，使得 $∠ A G D = ∠ B G C$ .

查看试题解析
21. 如图， $△ A B C$ 中， $A B = A C$ ， $E$ 在线段 $A C$ 上， $D$ 在 $A B$ 的延长线上，连 $D E$ 交 $B C$ 于 $F$ ，过 $E$ 作 $E G ⊥ B C$ 于 $G$ .

(1)、若 $∠ A = 50 °$ ， $∠ D = 30 °$ ，求 $∠ G E F$ 的度数；

(2)、若 $B D = C E$ ，求证： $F G = B F + G C$ .

查看试题解析
22. 某商店需要购进甲、乙两种商品共200件，其进价和售价如表：

甲

乙

进价（元/件）

14

35

售价（元/件）

20

45

(1)、若商店计划销售完这批商品后能获利1680元，问甲、乙两种商品应分别购进多少件？

(2)、若商店计划投入资金小于5320元，且销售完这批商品后获利大于1660元，请问有几种购货方案？并求出其中获利最大的购货方案.

查看试题解析
23. 问题背景：角平分线上的点到角两边的距离相等.若一个多边形的每个内角角平分线都交于一点 $O$ ，点 $O$ 叫做该多边形的内心，点 $O$ 到其中一边的距离叫做 $r$ .
问题解决：如图1，在面积为 $S$ 的 $△ A B C$ 中， $B C = a$ ， $A C = b$ ， $A B = c$ ，内心 $O$ 到边 $A C$ 的距离为 $r$ ，试说明 $r = \frac{2 S}{a + b + c}$ .

类比推理：如图2，存在内心 $O$ 的四边形 $A B C D$ 面积为 $S$ ，周长为 $l$ ，用含有 $S$ 与 $l$ 的式子表示内心 $O$ 到边 $A B$ 的距离 $r =$ ▲ ；

理解应用：如图3，在四边形 $A B C D$ 中， $A B / / D C$ ， $A B = 21$ ， $C D = 11$ ， $A D = B C = 13$ ，对角线 $B D = 20$ ，点 $O_{1}$ 与 $O_{2}$ 分别为 $△ A B D$ 与 $△ B C D$ 的内心，它们到各自三角形的边的距离分别为 $r_{1}$ 和 $r_{2}$ ，求 $\frac{r_{1}}{r_{2}}$ 的值.

查看试题解析
24. 如图，在等边 $△ A B C$ 中， $D$ 是直线 $B C$ 上一点， $E$ 是边 $A C$ 上一动点，以 $D E$ 为边作等边 $△ D E F$ ，连接 $C F$ .（提示：含 $30 °$ 的直角三角形三边之比为 $1 ： \sqrt{3} ： 2$ ）

(1)、如图1，若点 $D$ 在边 $B C$ 上，求证： $C E + C F = C D$ ；

(2)、如图2，若点 $D$ 在 $B C$ 的延长线上，请探究线段 $C E$ ， $C F$ 与 $C D$ 之间存在怎样的数量关系？并说明理由；

(3)、图2中，若 $E D = A C = 2 \sqrt{3}$ ，点 $E$ 从 $A$ 运动到 $C$ 停止，求出此过程中点 $F$ 运动的路径长.

查看试题解析

	甲	乙
进价（元/件）	14	35
售价（元/件）	20	45