湖北省武汉市东西湖区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-09-30 类型:期中考试
一、单选题
-
1. 下列四个图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形具有稳定性的是( )A、三角形 B、四边形 C、五边形 D、六边形3. 一定能确定△ABC≌△DEF的条件是( )A、AB=DE,BC=EF,∠A=∠D B、∠A=∠E,AB=EF,∠B=∠D C、∠A=∠D,AB=DE,∠B=∠E D、∠A=∠D,∠B=∠E,∠C=∠F4. 已知等腰三角形的一边长为4cm,周长是18cm,则它的腰长是( )A、4cm B、7cm C、10cm D、4cm或7cm5. 如图,乐乐书上的三角形墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是( )
2. 下列图形具有稳定性的是( )A、三角形 B、四边形 C、五边形 D、六边形3. 一定能确定△ABC≌△DEF的条件是( )A、AB=DE,BC=EF,∠A=∠D B、∠A=∠E,AB=EF,∠B=∠D C、∠A=∠D,AB=DE,∠B=∠E D、∠A=∠D,∠B=∠E,∠C=∠F4. 已知等腰三角形的一边长为4cm,周长是18cm,则它的腰长是( )A、4cm B、7cm C、10cm D、4cm或7cm5. 如图,乐乐书上的三角形墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是( ) A、 B、 C、 D、6. 用形状、大小完全相同的下列图形,不能进行平面嵌的是( )A、三角形 B、四边形 C、正五边形 D、正六边形7. 如图,把矩形 沿 对折后使两部分重合,若 ,则 =( )
A、 B、 C、 D、6. 用形状、大小完全相同的下列图形,不能进行平面嵌的是( )A、三角形 B、四边形 C、正五边形 D、正六边形7. 如图,把矩形 沿 对折后使两部分重合,若 ,则 =( )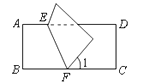 A、110° B、115° C、120° D、130°8. 如图的三角形纸片中,CB=8cm,AC=6cm,AB=5cm,沿过点C的直线折叠这个三角形,使点A落在CB边上的点E处,折痕为CD.则△BDE的周长是( )
A、110° B、115° C、120° D、130°8. 如图的三角形纸片中,CB=8cm,AC=6cm,AB=5cm,沿过点C的直线折叠这个三角形,使点A落在CB边上的点E处,折痕为CD.则△BDE的周长是( ) A、6cm B、7cm C、8cm D、5cm9. 一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是( )A、8 B、9 C、10 D、1110. 如图, 是等边三角形,F、G分别为AC和BC的中点,D在线段BG上,连接DF,以DF为边作等边 ,ED的延长线交AB于H.连接EC,则以下结论:① ;② ;③ ;④当D在线段BG上(不与G点重合)运动时, .其中正确的结论个数有( )
A、6cm B、7cm C、8cm D、5cm9. 一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是( )A、8 B、9 C、10 D、1110. 如图, 是等边三角形,F、G分别为AC和BC的中点,D在线段BG上,连接DF,以DF为边作等边 ,ED的延长线交AB于H.连接EC,则以下结论:① ;② ;③ ;④当D在线段BG上(不与G点重合)运动时, .其中正确的结论个数有( )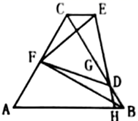 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在平面直角坐标系中,点 关于x轴对称的点的坐标为 .12. 若从一个多边形的一个顶点出发,最多可以引9条对角线,则它是边形.13. 如图是两个全等三角形,则 的大小是.
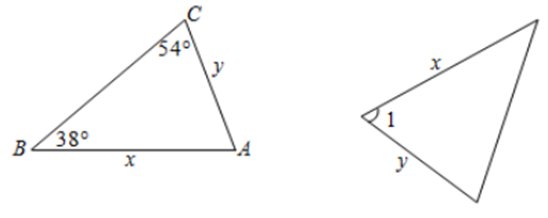 14. 已知 的周长为30,面积为20,其内角平分线交于点O,则点O到边BC的距离为.15. 如图,在四边形ABCD中, , ,EF分别是边BC,CD上的动点,当 的周长最小时, °.
14. 已知 的周长为30,面积为20,其内角平分线交于点O,则点O到边BC的距离为.15. 如图,在四边形ABCD中, , ,EF分别是边BC,CD上的动点,当 的周长最小时, °.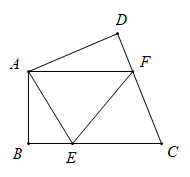 16. 在 中, , ,以CB为边作一个形状等边三角形 ,则DA的最大值是.
16. 在 中, , ,以CB为边作一个形状等边三角形 ,则DA的最大值是.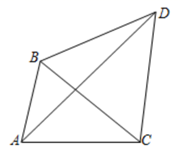
三、解答题
-
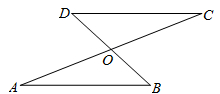
17. 如图,AC和BD相交于点0,OA=OC, OB=OD.求证:DC//AB
 18. 在 中,如果 ,那么你能判断 是什么三角形吗?19. 如图,在正方形网格中,每个小正方形的边长都为1, 在网格中的位置如图所示, 的三个顶点都在格点上.将点A、B、C的横坐标和纵坐标都乘以 ,分别得到点 、 、 .
18. 在 中,如果 ,那么你能判断 是什么三角形吗?19. 如图,在正方形网格中,每个小正方形的边长都为1, 在网格中的位置如图所示, 的三个顶点都在格点上.将点A、B、C的横坐标和纵坐标都乘以 ,分别得到点 、 、 . (1)、写出 ,三个顶点的坐标;(2)、若 与 关于x轴对称,在平面直角坐标系中画出 ;(3)、若以点A、C、P为顶点的三角形与 全等,直接写出所有符合条件的点P的坐标.20. 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.
(1)、写出 ,三个顶点的坐标;(2)、若 与 关于x轴对称,在平面直角坐标系中画出 ;(3)、若以点A、C、P为顶点的三角形与 全等,直接写出所有符合条件的点P的坐标.20. 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.求证:BE∥DF.
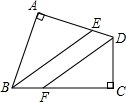 21. 如图,在△ABC中,AC=BC,∠ACB=90°,D为△ABC内一点, ∠BAD=15°,AD=AC,CE⊥AD于E,且CE=5.
21. 如图,在△ABC中,AC=BC,∠ACB=90°,D为△ABC内一点, ∠BAD=15°,AD=AC,CE⊥AD于E,且CE=5.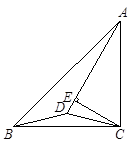 (1)、求BC的长;(2)、求证:BD=CD.22. 如图,在 中,点D,E分别在边AC,AB上,BD,CE交于点P,且 .
(1)、求BC的长;(2)、求证:BD=CD.22. 如图,在 中,点D,E分别在边AC,AB上,BD,CE交于点P,且 .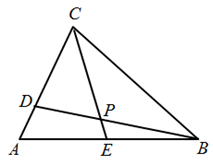 (1)、探究 与 的数量关系,并证明之;(2)、求证: .23. 在等腰 中, ,点D是AC上一动点,点E在的BD延长线上且 ,AF平分 交DE于点F连接FC.
(1)、探究 与 的数量关系,并证明之;(2)、求证: .23. 在等腰 中, ,点D是AC上一动点,点E在的BD延长线上且 ,AF平分 交DE于点F连接FC.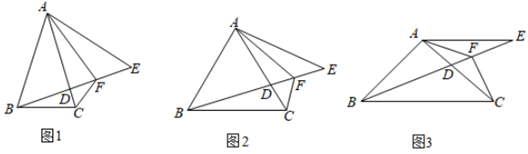 (1)、如图1,求证: ;(2)、如图2,当 时,求证: ;(3)、如图3,当 ,且 时,求证: .24. 如图,点 , ,且a、b满足 .
(1)、如图1,求证: ;(2)、如图2,当 时,求证: ;(3)、如图3,当 ,且 时,求证: .24. 如图,点 , ,且a、b满足 .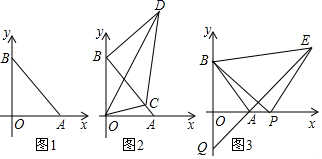 (1)、如图1,求 的面积;(2)、如图2,点C在线段AB上(不与A、B重合)移动, ,且 ,猜想线段AC、BD、CD之间的数量关系并证明你的结论;(3)、如图3,若P为x轴上异于原点O和点A的一个动点,连接PB,将线段PB绕点P顺时针旋转 至PE,直线AE交y轴于点Q,当P点在x轴上移动时,线段BE和线段BQ中哪一条线段长为定值,并求出该定值.
(1)、如图1,求 的面积;(2)、如图2,点C在线段AB上(不与A、B重合)移动, ,且 ,猜想线段AC、BD、CD之间的数量关系并证明你的结论;(3)、如图3,若P为x轴上异于原点O和点A的一个动点,连接PB,将线段PB绕点P顺时针旋转 至PE,直线AE交y轴于点Q,当P点在x轴上移动时,线段BE和线段BQ中哪一条线段长为定值,并求出该定值.