湖北省十堰市丹江口市2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-09-30 类型:期中考试
一、单选题
-
1. 下列图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )A、5 B、6 C、12 D、163. 要求画△ABC的边AB上的高,下列画法中,正确的是( )A、
2. 已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )A、5 B、6 C、12 D、163. 要求画△ABC的边AB上的高,下列画法中,正确的是( )A、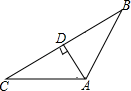 B、
B、 C、
C、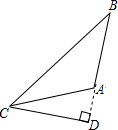 D、
D、 4. 若等腰三角形的顶角为 ,则它的底角度数为( )
4. 若等腰三角形的顶角为 ,则它的底角度数为( )
A、 B、 C、 D、5. 如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,则 的度数是( ) A、15° B、25° C、30° D、10°6. 如图,△ACB≌△A'CB',∠BCB'=25°,则∠ACA'的度数为( )
A、15° B、25° C、30° D、10°6. 如图,△ACB≌△A'CB',∠BCB'=25°,则∠ACA'的度数为( ) A、35° B、30° C、25° D、20°7. 如图,C是∠AOB的平分线上一点,添加下列条件不能判定△AOC≌△BOC的是( )
A、35° B、30° C、25° D、20°7. 如图,C是∠AOB的平分线上一点,添加下列条件不能判定△AOC≌△BOC的是( ) A、OA =OB B、AC=BC C、∠A=∠B D、∠1=∠28. 如图,DE是△ABC中AC边的垂直平分线,若BC=4cm,AB=5cm,则△EBC的周长为( )
A、OA =OB B、AC=BC C、∠A=∠B D、∠1=∠28. 如图,DE是△ABC中AC边的垂直平分线,若BC=4cm,AB=5cm,则△EBC的周长为( ) A、8cm B、9cm C、10cm D、11cm9. 如图,已知 ,∠OAB=30°,∠AOB=90°,O点与坐标系原点重合,若点P在坐标轴上,且 是等腰三角形,则点P的坐标可能有( )
A、8cm B、9cm C、10cm D、11cm9. 如图,已知 ,∠OAB=30°,∠AOB=90°,O点与坐标系原点重合,若点P在坐标轴上,且 是等腰三角形,则点P的坐标可能有( ) A、5个 B、6个 C、7个 D、8个10. 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论:
A、5个 B、6个 C、7个 D、8个10. 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论:①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE,④DE=DF.其中正确的是( )
 A、①②③ B、①②④ C、①② D、①③
A、①②③ B、①②④ C、①② D、①③二、填空题
-
11. 如图,要使四边形木架不变形,至少要钉上 根木条.
 12. 已知三角形两边长为2和7,则第三边a的取值范围为.13. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第块去,这利用了三角形全等中的原理.
12. 已知三角形两边长为2和7,则第三边a的取值范围为.13. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第块去,这利用了三角形全等中的原理.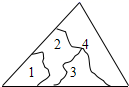 14. 如图,点D在BC上,AB=AD,∠C=∠E,∠BAD=∠CAE,若∠1+∠2=108°,则∠ABC的度数是.
14. 如图,点D在BC上,AB=AD,∠C=∠E,∠BAD=∠CAE,若∠1+∠2=108°,则∠ABC的度数是. 15. 如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=.
15. 如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=. 16. 如图,等腰△ABC底边BC的长为6cm,面积是24cm2 , 腰AB的垂直平分线MN交AB于点M,交AC于点N,若D为BC边上的中点,E为线段MN上一动点,则△BDE的周长最小值为cm.
16. 如图,等腰△ABC底边BC的长为6cm,面积是24cm2 , 腰AB的垂直平分线MN交AB于点M,交AC于点N,若D为BC边上的中点,E为线段MN上一动点,则△BDE的周长最小值为cm.
三、解答题
-
17. 已知一个多边形的内角和比其外角和的2倍多180°,求这个多边形的边数及对角线的条数?18. 如图,三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,求 的周长
 19. 如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
19. 如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3). (1)、请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);(2)、直接写出D,E,F三点的坐标:D( ),E( ),F( );(3)、在y轴上存在一点,使PC﹣PB最大,则点P的坐标为.20. 如图,已知AD是△ABC中BC边上的中线,且AD=BD=CD,试判断△ABC的形状.
(1)、请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);(2)、直接写出D,E,F三点的坐标:D( ),E( ),F( );(3)、在y轴上存在一点,使PC﹣PB最大,则点P的坐标为.20. 如图,已知AD是△ABC中BC边上的中线,且AD=BD=CD,试判断△ABC的形状. 21. 已知:如图,AB=CD,DE=BF,AE=CF.
21. 已知:如图,AB=CD,DE=BF,AE=CF. (1)、求证:△ABE≌△CDF;(2)、判断AE与CF的位置关系,并说明理由.22. 如图,△ABC中,∠A=90°,∠B=60°,BC的垂直平分线交BC与点D,交AC于点E.
(1)、求证:△ABE≌△CDF;(2)、判断AE与CF的位置关系,并说明理由.22. 如图,△ABC中,∠A=90°,∠B=60°,BC的垂直平分线交BC与点D,交AC于点E.
求证:
(1)、AE=DE;(2)、若AE=6,求CE的长.23.(1)、如图①,已知OA=OB,AC∥BD,求证:AC=BD; (2)、如图,已知,AD是△ABC中BC边上的中线,AB∥EC,∠BAD=∠EAD.试探究线段AB与AE、CE之间的数量关系,并证明你的结论.
(2)、如图,已知,AD是△ABC中BC边上的中线,AB∥EC,∠BAD=∠EAD.试探究线段AB与AE、CE之间的数量关系,并证明你的结论. 24. 如图
24. 如图 (1)、如图①,点D,E分别在等边△ABC的边BC,AB上,且AE=BD,连接AD,CE交于点F.找出图中与△ABD全等的三角形,证明并求出∠AFE的度数;(2)、如图②,若(1)中的点D,E分别在等边△ABC的边BC,AB延长线上,(1)中的结论是否仍然成立?请说明理由.25. 如图①,等腰直角三角形ABC的直角顶点A在y轴上,B点在x轴上,C点在第一象限,已知A(0,a),B(b,0),且a,b满足 .
(1)、如图①,点D,E分别在等边△ABC的边BC,AB上,且AE=BD,连接AD,CE交于点F.找出图中与△ABD全等的三角形,证明并求出∠AFE的度数;(2)、如图②,若(1)中的点D,E分别在等边△ABC的边BC,AB延长线上,(1)中的结论是否仍然成立?请说明理由.25. 如图①,等腰直角三角形ABC的直角顶点A在y轴上,B点在x轴上,C点在第一象限,已知A(0,a),B(b,0),且a,b满足 .
 (1)、求A,B的坐标;(2)、求点C的坐标;(3)、如图②,点D是BC上的动点,以点A为直角顶点,AD为腰作等腰直角三角形ADE,使E点落在第一象限,试问:当D点在BC上运动时,∠ECD的大小是否改变?若不变,请求出∠ACE的度数;若改变,请说明理由.
(1)、求A,B的坐标;(2)、求点C的坐标;(3)、如图②,点D是BC上的动点,以点A为直角顶点,AD为腰作等腰直角三角形ADE,使E点落在第一象限,试问:当D点在BC上运动时,∠ECD的大小是否改变?若不变,请求出∠ACE的度数;若改变,请说明理由.