湖北省鄂州市鄂城区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2021-09-30 类型：期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知四组线段的长分别如下，以各组线段为边，不能组成三角形的是（ ）A、1，2，3 B、2，3，4 C、3，4，5 D、2，2，23. 下列判断中错误的是（ ）A、有两角和其中一个角的对边对应相等的两个三角形全等 B、有一边相等的两个等边三角形全等 C、有两边和一角对应相等的两个三角形全等 D、有两边和其中一边上的中线对应相等的两个三角形全等4. 在平面直角坐标系中，点P（3，0）关于y轴对称的点的坐标是（ ）A、（0，3） B、（-3，0） C、（0，-3） D、（3，0）5. 如图，在△ABC中，AB＝AC，AD是边BC上的高，E，F是AD上的两点，且AE=EF=FD. 若△ABC的面积为6 cm2 ， 则图中阴影部分的面积是（ ）cm2.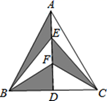
A、2 B、3 C、4.8 D、56. 如图，在△ABC中，沿直线DE折叠后，使得点B与点A重合，已知AC=8 cm，△ADC的周长为18 cm，则BC的长为（ ）
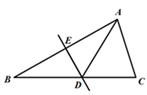A、8 cm B、10 cm C、18 cm D、26 cm7. 如图为6个边长相等的正方形的组合图形，则∠1+∠3-∠2=（ ）
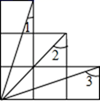A、30° B、45° C、60° D、135°8. 如图，为了促进当地旅游发展，某地要在三条公路AB，AC，BC两两相交围成的一块平地内修建一个度假村.要使这个度假村到三条公路的距离相等，则度假村应该修在何处？可供选择的位置有（ ）处.
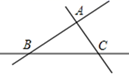A、一 B、二 C、三 D、四9. 如图，△ABC的外角∠ACD的平分线CQ与内角∠ABC的平分线BQ交于点Q，若∠BQC=36°，则∠CAQ的度数为（ ）
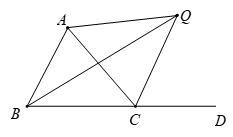A、54° B、62° C、72° D、75°10. 如图，AD 为等腰△ABC的高，其中∠ACB=50°，AC=BC，E，F 分别为线段AD，AC 上的动点，且 AE=CF， 当 BF＋CE 取最小值时，∠AFB的度数为（ ）
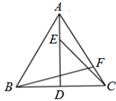A、75° B、90° C、95° D、105°二、填空题
-
11. 如图，为了使一扇旧木门不变形，木工师傅在木门的背后加钉了一根木条，这样做的道理是 ．
12. 如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于点D，DE⊥AB，垂足为E，且AB＝3 cm，则△DEB的周长为cm.
13. 一个多边形的内角和是外角和的3倍，这个多边形的对角线有条.14. 如果等腰三角形的一腰上的高等于腰长的一半，则其一个底角的度数是 .15. 已知△ABC中，AD是△ABC的中线，AB=4，AD=5，则边AC的取值范围是 .16. 等边△ACD和等边△BCE有一个公共顶点C，直线AE与BD交于点F ，直线AE与CD交于点G， 直线CE与BD交于点H，连接GH. 下列结论：①AE=DB；②△BHC≌△EGC；③∠DFA=60°；④△HGC为等边三角形. 其中正确的结论有.（填序号）
三、解答题
-
17. 如图，将六边形纸片ABCDEF沿虚线剪去一个角（∠BCD）后，得到∠1＋∠2＋∠3＋∠4＋∠5＝400°.
(1)、求六边形ABCDEF的内角和；(2)、求∠BGD的度数.18. 如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D.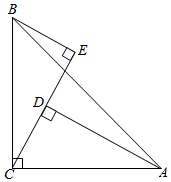
(1)、求证∠BCE=∠CAD；(2)、若AD=12 cm，DE=7 cm，求BE.19. 如图，点E在AB上，AC与DE相交于点F，△ABC≌△DEC，∠B=65°.
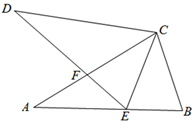(1)、求∠DCA的度数；(2)、若∠A=20°，求∠DFA的度数.20. 如图，△ABC中，AC的垂直平分线DE交AC于点E，交∠ABC的平分线于点D，DF⊥BC于点F，连接AD.
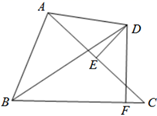(1)、求证AB+CF=BF；(2)、若∠ABC=70°，求∠DAE的度数.21. 如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（-2，3），B（-2，1），C（-1，1）.
(1)、画出△ABC关于x轴对称的△A1B1C1 ， 并写出点A1的坐标为 ▲ ；(2)、直接写出点B关于直线n（直线n上各点的纵坐标都为-1）对称的点B′的坐标为；(3)、在y轴上找一点P，使PA+PB的值最小，保留作图痕迹，并直接写出点P的坐标为 ▲ .22. 已知△ABC，∠BAC的平分线上有一点O，且OB=OC.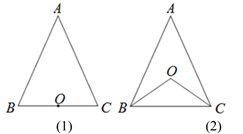
(1)、如图(1)，若点O在边BC上，求证：△ABC是等腰三角形；(2)、如图(2)，若点O在△ABC内部，求证AB=AC；(3)、若点O在△ABC外部，AB=AC还一定成立吗？请直接写出你的判断，无需说明理由23. 如图所示，已知△ABC中，∠B=∠C，AB=4厘米，BC=3厘米，点D为AB的中点.如果点P在线段BC上以每秒1厘米的速度由点B向点C运动，同时，点Q在线段CA上以每秒a厘米的速度由点C向点A运动，设运动时间为t（秒）（0≤t≤3）.
(1)、用含t的式子表示PC的长度是；(2)、若点P，Q的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；(3)、若点P，Q的运动速度不相等，当点Q的运动速度a为多少时，能够使△BPD与△CQP全等？24. 如图(1)，在平面直角坐标系中，A（2，0），B（0，4），以A为直角顶点，AB为腰作等腰Rt△ABC，使点C落在第三象限.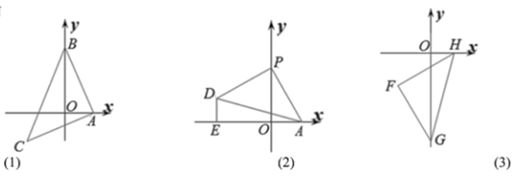
(1)、求点C的坐标；(2)、如图(2)，P是y轴正半轴上一动点，连接AP，以P为直角顶点，PA为腰作等腰Rt ，且点D在x轴上方，过点D作DE⊥x轴于点E，求 的值；(3)、如图(3)，点F的坐标为（-3，-3），点G（0，m）是y轴负半轴上一动点，连接FG，作 ，交x轴正半轴于点H（n，0），当点G运动时， 的值是否发生变化？如果不变，求其值；如果变化，请说明理由.