吉林省白城市通榆县2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-09-30 类型：月考试卷

进入 出卷网 下载

一、单项选择题(每小题2分，共12分)

  • 1. 二次函数y=(x-1)2+3的顶点坐标是（    ）
    A、(1，3) B、(1，-3) C、(-1，3) D、(-1，-3)

    查看试题解析

  • 2. 方程x2-3x+2=0的根的情况是（    ）
    A、只有一个实数根 B、没有实数根 C、有两个不相等的实数根 D、有两个相等的实数根

    查看试题解析

  • 3. 一元二次方程x2-4x-1=0配方后可化为（    ）
    A、(x+2)2=3 B、(x+2)2=5 C、(x-2)2=3 D、(x-2)2=5

    查看试题解析

  • 4. 二次函数y=ax2+bx+c的图像如图所示，根据图像可得a，b，c与0的大小关系是（   ）

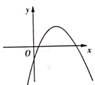    A、a>0，b<0，c<0 B、a>0，b>0，c>0 C、a<0，b<Q，c<0 D、a<0，b>0，c<0

    查看试题解析

  • 5. 将抛物线y=x2向右平移1个单位长度后，所得到的抛物线的解析式是（    ）
    A、y=x2-1 B、y=x2-1 C、y=(x-1)2 D、y=(x+1)2

    查看试题解析

  • 6. 为庆祝建党100周年华诞，某校组织摄影比赛，小明上交的作品是一张七寸照片(长7英寸，宽5英寸)，现将照片贴在一张矩形衬纸的正中央，照片四周外露衬纸的宽度相同，矩形衬纸的面积为照片面积的3倍，设照片四周外露衬纸的宽度为x英寸(如图)，下面所列方程正确的是（    ）

    A、(7+2x)(5+2x)=3×7×5 B、3(7+x)(5+x)=7×5 C、3(7+2x)(5+2x)=7×5 D、(7+x)(5+x)=3×7×5

    查看试题解析

二、填空题(每小题3分，共24分)

  • 7. 一元二次方程x(x-1)=0的两个根分别为

    查看试题解析

  • 8. 二次函数y= −12 (x-3)2的图像的开口方向是(填“向上”或“向下")．

    查看试题解析

  • 9. 若关于x的一元二次方程(x+3)2=p有实数根，则p的值可以为(写出一个即可)．

    查看试题解析

  • 10. 者关于上的一元二次方程x2+3x-m=0有两个相等的实数根，则m的值为

    查看试题解析

  • 11. 抛物线y=(x+2)(x-1)的对称轴是直线

    查看试题解析

  • 12. 已知点(-1，y1)，(2，y2)在抛物线y=x2-2x+c上，则y1 ， y2的大小关系．是

    查看试题解析

  • 13. 如图，直线AB与抛物线y=ax2+bx+c(a>0)相交于A(-2，5)，B(5，12)两点，点P是抛物线上位于直线AB下方的点，则点P的横坐标m的取值范围是

    查看试题解析

  • 14. 如图，正方形ABCD的边长是4，E是AB上一点，F是AD延长线上的一点，BE=DF。若四边形AEGF是矩形，则矩形AEGF的面积y关于BE的长的函数解析式是(不用写出x的取值范围)

    查看试题解析

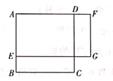
三、解答题(每小题5分，共20分)

四、解答题(每小题7分，共28分)

  • 19. 已知关于x的一元二次方程x2-2x+k+2=0
    (1)、若k=-6，求此方程的解
    (2)、若该方程无实数根，求k的取值范围．

    查看试题解析

  • 20. 2021年是中国共产党建党100周年，全国各地积极开展“弘扬红色文化，重走长征路”主题教育学习活动，某市“红二方面军长征出发地纪念馆”成为重要的活动基地，据了解，今年3月份该基地接待参观人数为10万人，5月份接待参观人数增加到12.1万人
    (1)、求这两个月参观人数的月平均增长率
    (2)、按照这个增长率，预计6月份的参观人数是多少？

    查看试题解析

  • 21. 2021年7月1是建党100周年纪念日，在本月日历表上可以用一个方低圆出4个数(如图所示)，若圈出的四个数中，最小数与最大数的乘积为65，求这个最小数(请用方程知识解答)。

    查看试题解析

  • 22. 对于抛物线y=x2-4x+3

    (1)、将抛物线的解析式化为顶点式
    (2)、E坐标系中利用五点法画出此抛物线

    x

    ……

    ……

    y

    ……

    ……
    (3)、指出当x取什么值时，函数的值y随x的增大而增大？

    查看试题解析

五、解答题(每小题8分，共16分)

  • 23. 水果店张阿姨以每千克2元的价格购进某种水果若干千克，然后以每千克4元的价格出例，每天可售出100下克，通过调查发现，这种水果的售价每降低0.1元，每天可多售出20千克，为保证每天至少售出260千克，张阿姨决定降价销售。
    (1)、若将这种水果每下克的售价降低x元，则每天的销售量是千克(用含x的代数式表示)。
    (2)、若销售这种水果要想每天盈利300元，则张阿姨需将每下克的售价降低多少元？

    查看试题解析

  • 24. 如图，在平面直角坐标系中，直线y=x+4与坐标轴分别交于A，B两点，过A，B两点的抛物线为y=-x2+bx+c，点D为线段AB上一动点，过点D作CD垂直x轴于点C，交抛物线于点E。

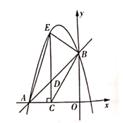    (1)、求抛物线的解析式．
    (2)、当DE=4时，求四边形CAEB的面积。

    查看试题解析

六、解答题(每小题10分，共20分)

  • 25. 如图，在△ABC中。∠A=90°，AB=12cm，AC=8cm，现有动点P从点B出发，沿射线BA方向运动，动点Q从点C出发，沿射线CA方向运动，已知点P的速度是2cm/s，点Q的速度是1cm/s，它们同时出发，设运动时间是t(s)(t>0)

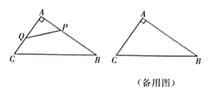    (1)、当t=4时，求△APQ的面积．
    (2)、经过多少秒时，△APQ的面积是△ABC面积的一半。

    查看试题解析

  • 26. 如图，抛物线y=x2+bx+c与x轴相交于A、B两点，与轴相交于点C，对称轴为直线x=2，顶点为D，点B的坐标为(3，0)。

    (1)、点A的坐标为 。
    (2)、求此抛物线的解析式与点D的坐标。
    (3)、若P是抛物线上一动点。是否存在点P，使S△PAB= 13 S△CAB若存在。谢求出所有点P的坐标；若不存在，请说明理由。
    (4)、当二次函数y=x2+bx+c的自变量x满足m≤x≤m+2时，函数y的最小值为 54 ，直接写出m的值。

    查看试题解析