天津市滨海新区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列标志中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知三角形的两边长分别为3cm、5cm，则此三角形第三边的长可以是（）

A、1cm B、5cm C、8cm D、9cm

查看试题解析
3. 若分式 $\frac{x - 1}{2 x + 1}$ 的值为0，则x的值是（）

A、0 B、-1 C、1 D、3

查看试题解析
4. 一组数据：5，8，6，3，4的中位数是（）

A、5 B、6 C、4 D、8

查看试题解析
5. 在下列多项式的乘法中，可以用平方差公式计算的是（）

A、 $(2 x + y) (2 y - x)$ B、 $(\frac{1}{2} x + 1) (- \frac{1}{2} x - 1)$ C、 $(3 x - y) (3 x + y)$ D、 $(x - y) (- x + y)$

查看试题解析
6. 如图，已知AB＝DB ， BC＝BE ， $∠ 1 = ∠ 2$ ，由这三个条件，就可得出△ABE≌△DBC ，依据的判定方法是（）

A、边边边 B、边角边 C、角边角 D、角角边

查看试题解析
7. 一个多边形内角和等于1080°，则这个多边形的边数是（）

A、6 B、8 C、10 D、12

查看试题解析
8. 下列计算正确的是（）

A、 ${{(x}^{3})}^{2} {=x}^{6}$ B、 ${(x y)}^{^{2}} = x y^{2}$ C、 $x^{2} \cdot x^{3} = x^{6}$ D、 $x^{6} \div x^{2} = x^{3}$

查看试题解析
9. 多项式 $8 a^{3} b^{2} + 12 a^{3} b c - 4 a^{2} b$ 中，各项的公因式是（）

A、 $a^{2} b$ B、 $- 4 a^{2} b^{2}$ C、 $4 a^{2} b$ D、 $- a^{2} b$

查看试题解析
10. 下列式子从左到右变形是因式分解的是（）

A、 $a^{2} + 4 a - 21 = a (a + 4) - 21$ B、 $a^{2} + 4 a - 21 = (a - 3) (a + 7)$ C、 $(a - 3) (a + 7) = a^{2} + 4 a - 21$ D、 $a^{2} + 4 a - 21 = {(a + 2)}^{2} - 25$

查看试题解析
11. 为备战2022年北京冬奥会，甲、乙两名运动员训练测验，两名运动员的平均分相同，且 $s_{甲}^{2}$ =0.01， $s_{乙}^{2}$ =0.006，则成绩较稳定的是（）

A、乙运动员 B、甲运动员 C、两运动员一样稳定 D、无法确定

查看试题解析
12. 如图， $△ A B C$ 为等边三角形，点D、E分别在边 $A C$ 和 $A B$ 上， $A E = C D$ ， $C E$ 与 $B D$ 交于点P， $B F ⊥ C E$ 于点F，若 $A P ⊥ B P$ ，则下列结论：① $∠ A C E = ∠ C B D$ ，② $∠ B P E = 60 °$ ，③ $△ A P B ≌ △ B F C$ ，其中正确的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

13. 如图，CE是△ABC的外角∠ACD的平分线，若∠B=35°，∠ACE=60°，则∠A= ．

查看试题解析
14. 如图，已知在△ABC中，∠B与∠C的平分线交于点P．当∠A = 70°时，则∠BPC的度数为．

查看试题解析
15. 广播电视局欲招聘播音员一名，对甲、乙两名候选人进行了两项素质测试，两人的两项测试成绩如下表所示.根据需要，广播电视局将面试、综合知识测试的成绩按3︰2的比确定两人的平均成绩，那么将被录取．

测试项目

测试成绩

甲

乙

面试

90

95

综合知识测试

85

80

查看试题解析
16. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A D$ 平分 $∠ C A B$ ， $D E ⊥ A B$ 于E， $∠ B = 30 °$ ，若 $D E$ =2，则 $C B$ 的长等于．

查看试题解析
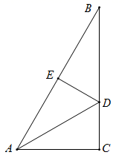17. 如图，等腰三角形ABC底边BC的长为4cm ，面积是12cm² ， D为BC边上的中点，腰AB的垂直平分线EF交AD于M ，交AC于点F ，则BM+DM的值为cm ．

查看试题解析
18. 如图，AB=AC ， BD⊥AC于点D ，点E ， F分别为AB ， BD上的动点，且AE=BF ， ∠DBA=34°．

(1)、CE与BD的大小关系（填“≥”或“≤”）；

(2)、当CE+AF取得最小值时，∠BEC的度数是．

查看试题解析

三、解答题

19.

(1)、计算： $(6 x^{4} - 8 x^{3}) \div (- 2 x^{2})$ ；

(2)、计算： $(x - 8 y) (x - y)$ ；

(3)、因式分解： $3 m x^{2} + 6 m x y + 3 m y^{2}$ ．

查看试题解析
20.

(1)、计算： $(a^{2} - 16) \div \frac{a + 4}{a - 4}$ ；

(2)、解分式方程： $1 - \frac{1}{x - 4} = \frac{5 - x}{x - 4}$ ．

查看试题解析
21. 当今，青少年视力水平下降已引起全社会的关注，为了了解某市30000名学生的视力情况，从中抽取了一部分学生进行了一次抽样调查，利用所得数据绘制的频数分布直方图如下：解答下列问题：（学生的视力结果保留到小数点后一位）

(1)、本次抽样调查共抽测了名学生；

(2)、参加抽测的学生的视力的众数在范围内；中位数在范围内；

(3)、若视力为4.9及以上为正常，试估计该市学生的视力正常的人数约为多少？

查看试题解析
22. 如图，已知A(0，4)，B(－2，2)，C(3，0)．

(1)、作△ABC关于x轴对称的△A₁B₁C₁；

(2)、写出A₁ ， B₁ ， C₁的坐标．

查看试题解析
23. 两个小组同时开始攀登一座450m高的山，第一组的攀登速度是第二组的1.2倍，他们比第二组早1.5min到达峰顶．两个小组的攀登速度各是多少？

(1)、设第二组的攀登速度为x m/min，根据题意，用含有x的式子填写下表：

速度( m/min)

时间（min）

距离( m)

第一组

1.2x

450

第二组

x

450

(2)、列出方程，并求出问题的解．

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D 、 E 、 F$ 分别在边 $A B 、 B C 、 A C$ 上，且 $B E = C F ， E C = B D$ ．

(1)、求证： $△ B D E ≌ △ C E F$ ；

(2)、当 $∠ A = 40 °$ 时，求 $∠ D E F$ 的度数；

(3)、请你猜想：当 $∠ A$ 为多少度时， $∠ E D F + ∠ E F D = 120 °$ ，并请说明理由．

查看试题解析
25. 在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ， $A E$ 平分 $∠ B A C$ 交 $B C$ 于点E， $B D ⊥ A E$ 交 $A E$ 延长线于点D，连接 $C D$ ，过点C作 $C F ⊥ C D$ 交 $A D$ 于F．

(1)、如图①，①求 $∠ E B D$ 的度数；
②求证： $A F = B D$ ；

(2)、如图②， $D M ⊥ A C$ 交 $A C$ 的延长线于点M，探究 $A B 、 A C 、 A M$ 之间的数量关系，并给出证明．

查看试题解析

测试项目	测试成绩
测试项目	甲	乙
面试	90	95
综合知识测试	85	80

	速度( m/min)	时间（min）	距离( m)
第一组	1.2x		450
第二组	x		450