河北省唐山市古冶区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式是最简二次根式的是（）

A、 $\sqrt{13}$ B、 $\sqrt{12}$ C、 $\sqrt{3^{2}}$ D、 $\sqrt{\frac{2}{3}}$

查看试题解析
3. 如图，将一副三角尺按如图所示的方式摆放，则 $∠ α =$ （）

A、 $45 °$ B、 $60 °$ C、 $75 °$ D、 $90 °$

查看试题解析
4. 计算 $\frac{x}{{(x + 1)}^{2}} + \frac{1}{{(x + 1)}^{2}}$ 的结果是（）

A、1 B、 $\frac{1}{x + 1}$ C、x+1 D、 $\frac{1}{{(x + 1)}^{2}}$

查看试题解析
5. 四边形没有稳定性，当一个四边形的形状发生改变时，发生变化的是（）

A、四边形的外角和 B、四边形的边长 C、四边形的周长 D、四边形某些角的大小

查看试题解析
6. 六边形的内角和为（）

A、360° B、540° C、720° D、1080°

查看试题解析
7. 下列等式成立的是（）

A、 $3 + 4 \sqrt{2} = 7 \sqrt{2}$ B、 $\sqrt{3} \times \sqrt{2} = \sqrt{5}$ C、 $\sqrt{{(- 3)}^{2}} = 3$ D、 $\sqrt{3} \div \frac{1}{\sqrt{6}} = 2 \sqrt{3}$

查看试题解析
8. 如图1，已知 $∠ A B C$ ，用尺规作它的角平分线．
如图2，步骤如下，

第一步：以B为圆心，以a为半径画弧，分别交射线 BA ， BC 于点D，E；

第二步：分别以D，E为圆心，以b为半径画弧，两弧在 $∠ A B C$ 内部交于点P；

第三步：画射线 BP ．射线 BP 即为所求．

下列正确的是（）

A、a，b均无限制 B、 $a > 0$ ， $b > \frac{1}{2} D E$ 的长 C、a有最小限制，b无限制 D、 $a \geq 0$ ， $b < \frac{1}{2} D E$ 的长

查看试题解析
9. 若 $a \neq b$ ，则下列分式化简正确的是（）

A、 $\frac{a + 2}{b + 2} = \frac{a}{b}$ B、 $\frac{a - 2}{b - 2} = \frac{a}{b}$ C、 $\frac{a^{2}}{b^{2}} = \frac{a}{b}$ D、 $\frac{\frac{1}{2} a}{\frac{1}{2} b} = \frac{a}{b}$

查看试题解析
10. 如图，C岛在A岛的北偏东 $35 °$ 方向，B岛在A岛的北偏东 $80 °$ 方向，C岛在B岛的北偏西 $55 °$ 方向，则A，B，C三岛组成一个（）

A、等腰直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形

查看试题解析
11. 设 ${(2 a + b)}^{2} = {(2 a - b)}^{2} + A$ ，则 $A =$ （）

A、 $8 a b$ B、 $6 a b$ C、 $4 a b$ D、0

查看试题解析
12. 某工厂计划每天生产x吨生产资料，采用新技术后每天多生产3吨，实际生产180吨与原计划生产120吨的时间相等，那么适合x的方程是（　　）

A、 $\frac{120}{x + 3} = \frac{180}{x}$ B、 $\frac{120}{x - 3} = \frac{180}{x}$ C、 $\frac{120}{x} = \frac{180}{x + 3}$ D、 $\frac{120}{x} = \frac{180}{x - 3}$

查看试题解析
13. 关于x的分式方程 $\frac{5}{x} = \frac{a}{x - 2}$ 有解，则字母a的取值范围是（）

A、 $a = 2$ 或 $a = 0$ B、 $a \neq 0$ C、 $a \neq 5$ D、 $a \neq 5$ 且 $a \neq 0$

查看试题解析
14. $△ A B C$ 中， $A B = 2$ ， $A C = \sqrt{6}$ ， $∠ A B C = 60 °$ ， $∠ A C B = 45 °$ ，D为 $B C$ 的中点，直线l经过点D，过B作 $B F ⊥ l$ 于F，过A作 $A E ⊥ l$ 于E．则 $A E + B F$ 的最大值为（）

A、2 B、 $\sqrt{6}$ C、 $2 \sqrt{2}$ D、4

查看试题解析

二、填空题

15. 要使二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
16. 将0.00000034用科学记数法表示应为．

查看试题解析
17. 如图，在一个池塘两旁有一条笔直小路（B，C为小路端点）和一棵小树（A为小树位置）．测得的相关数据为： $∠ A B C = 60 °$ ， $∠ A C B = 60 °$ ， $B C = 58$ 米，则 $A C =$ 米．

查看试题解析
18. 如图， $△ A B C$ 是等边三角形，D为 $△ A B C$ 内一点， $D B = D A$ ， $B F = A B$ ， $∠ 1 = ∠ 2$ ，则 $∠ B F D =$ $°$ ．

查看试题解析

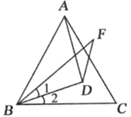
三、解答题

19. 计算：

(1)、 $\sqrt{8} + 3 \sqrt{2} - \sqrt{18}$ ；

(2)、 $(\sqrt{6} - 1) (\sqrt{6} + 1) + {(- 2)}^{0}$

查看试题解析
20. 解方程： $\frac{2}{x + 3} = \frac{1}{2 x}$

查看试题解析
21. 如图，已知 $A B = 4$ ， $A C = 7$ ．

(1)、用尺规作 $B C$ 边的垂直平分线；（保留作图痕迹，不写作法）

(2)、若 $B C$ 边的垂直平分线交 $A C$ 于D、交 $B C$ 于E；
①连接 $B D$ ，求 $△ A B D$ 的周长；

②若 $∠ A D B = 52 °$ ，求 $∠ D B C$ 的度数．

查看试题解析
22. 化简并求值：(1－ $\frac{2}{x + 1}$ )÷ $\frac{x^{2} - 1}{2 x + 2}$ ，其中x= $\sqrt{2}$ －1

查看试题解析
23. 我们已经学过将一个多项式分解因式的方法有提公因式法和公式法，其实分解因式方法还有分组分解法、拆项法、十字相乘法等等．
①分组分解法：将一个多项式适当分组后，可提公因式或运用公式继续分解的方法．请阅读以下例题：

例1． $a x + b y + b x + a y = (a x + b x) + (a y + b y) = x (a + b) + y (a + b) = (a + b) (x + y)$

例2． $2 x y + y^{2} - 1 + x^{2} = x^{2} + 2 x y + y^{2} - 1 = {(x + y)}^{2} - 1 = (x + y + 1) (x + y - 1)$

②拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法．请阅读以下例题：

例1． $x^{2} + 2 x - 3 = x^{2} + 2 x + 1 - 4 = {(x + 1)}^{2} - 2^{2} = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$

请你仿照以上例题的方法，解决下列问题：

(1)、分解因式： $x^{2} - n^{2} + x - n$ ；

(2)、分解因式： $a^{2} + 4 a + 3$ ．

查看试题解析
24. 某学校拟购进甲、乙两种规格的书柜放置新购买的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%，用5400元购进的甲种书柜的数量比用6300元购进乙种书柜的数量少6个.

(1)、每个甲种书柜的进价是多少元？

(2)、若该校拟购进这两种规格的书柜共60个，其中乙种书柜的数量不大于甲种书柜数量的 $2$ 倍.该校应如何进货使得购进书柜所需费用最少？

查看试题解析
25. 已知直线m，n相交于点B，点A，C分别为直线m，n上的点， $A B = B C = 1$ ，且 $∠ A B C = 60 °$ ，点E是直线m上的一个动点，点D是直线n上的一个动点，运动过程中始终满足 $D E = C E$ ．

(1)、如图1，当点E运动到线段 $A B$ 的中点，点D在线段 $C B$ 的延长线上时，求 $B D$ 的长．

(2)、如图2，当点E在线段 $A B$ 上运动，点D在线段 $C B$ 的延长线上时，求证： $B D = A E$ ．

查看试题解析