河北省石家庄市高邑县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-30 类型:期末考试
一、单选题
-
1. 若 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 约分: ( )A、 B、 C、 D、3. , , , , , , (相邻两个 之间依次多一个 )中,无理数的个数是( )A、 个 B、 个 C、 个 D、 个4. 图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )
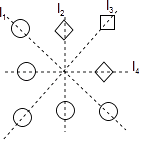 A、l1 B、l2 C、l3 D、l45. 下列计算正确的是( )A、 B、 C、 D、6. 下列条件中,不能判定 是直角三角形的是( )A、 B、 C、 D、7. 如果关于x的方程 无解,则m的值是( )A、2 B、0 C、1 D、–28. 若将实数 , , , 这四个数分别表示在数轴上,则其中可能被如图所示的墨迹覆盖的数是( ).
A、l1 B、l2 C、l3 D、l45. 下列计算正确的是( )A、 B、 C、 D、6. 下列条件中,不能判定 是直角三角形的是( )A、 B、 C、 D、7. 如果关于x的方程 无解,则m的值是( )A、2 B、0 C、1 D、–28. 若将实数 , , , 这四个数分别表示在数轴上,则其中可能被如图所示的墨迹覆盖的数是( ). A、 B、 C、 D、9.
A、 B、 C、 D、9.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
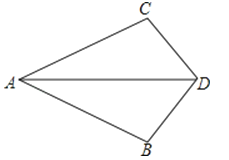 A、BD=CD B、AB=AC C、∠B=∠C D、∠BAD=∠CAD10. 如图,在等腰 中, , 与 的平分线交于点O,过点O做 ,分别交 、 于点D、E,若 的周长为18,则 的长是( )
A、BD=CD B、AB=AC C、∠B=∠C D、∠BAD=∠CAD10. 如图,在等腰 中, , 与 的平分线交于点O,过点O做 ,分别交 、 于点D、E,若 的周长为18,则 的长是( )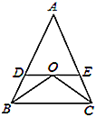 A、8 B、9 C、10 D、1211. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A、8 B、9 C、10 D、1211. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )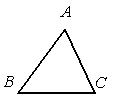 A、
A、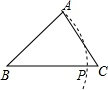 B、
B、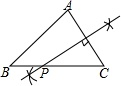 C、
C、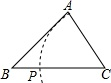 D、
D、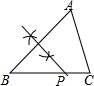 12. 如图,数轴上A,B两点对应的实数分别是1和 ,若A点关于B点的对称点为点C,则点C所对应的实数为( )
12. 如图,数轴上A,B两点对应的实数分别是1和 ,若A点关于B点的对称点为点C,则点C所对应的实数为( )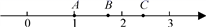 A、2 -1 B、1+ C、2+ D、2 +113. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A、2 -1 B、1+ C、2+ D、2 +113. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )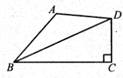 A、24 B、30 C、36 D、4214. 如图,在 中, , 是 的两条中线, 是 上一个动点,则下列线段的长度等于 最小值的是( )
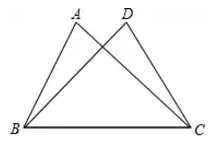
A、24 B、30 C、36 D、4214. 如图,在 中, , 是 的两条中线, 是 上一个动点,则下列线段的长度等于 最小值的是( ) A、2 B、 C、1 D、15. 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①AF=AC;②DF=CF;③∠AFC=∠C;④∠BFD=∠CAF.
A、2 B、 C、1 D、15. 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①AF=AC;②DF=CF;③∠AFC=∠C;④∠BFD=∠CAF.其中正确的结论个数有. ( )
 A、4个 B、3个 C、2个 D、1个16. 某校举行“停课不停学,名师陪你在家学”活动,计划投资8000元建设几间直播教室,为了保证教学质量,实际每间建设费用增加了20%,并比原计划多建设了一间直播教室,总投资追加了4000元.根据题意,求出原计划每间直播教室的建设费用是( )A、1600元 B、1800元 C、2000元 D、2400元
A、4个 B、3个 C、2个 D、1个16. 某校举行“停课不停学,名师陪你在家学”活动,计划投资8000元建设几间直播教室,为了保证教学质量,实际每间建设费用增加了20%,并比原计划多建设了一间直播教室,总投资追加了4000元.根据题意,求出原计划每间直播教室的建设费用是( )A、1600元 B、1800元 C、2000元 D、2400元二、填空题
-
17. 化简: 的结果为 .18. 如图 , , , 则的度数为 .
 19. 如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE , 且D点落在对角线D′处.若AB=3,AD=4,则ED的长为 .
19. 如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE , 且D点落在对角线D′处.若AB=3,AD=4,则ED的长为 .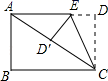 20. 对于实数a、b,定义一种新运算“ ”为: ,这里等式右边是实数运算.例如: ,则方程 的解是 .
20. 对于实数a、b,定义一种新运算“ ”为: ,这里等式右边是实数运算.例如: ,则方程 的解是 .三、解答题
-
21.(1)、计算: .(2)、化简并求值: ,其中 .(3)、解方程: .22. 如图, AB=CD,AE⊥BC于E,DF⊥BC于F,AE=DF.
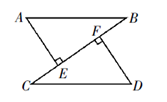
求证:
(1)、CE=BF;(2)、AB//CD.23. 某高速公路的同一侧有A,B两个城镇,如图所示,它们到高速公路所在直线 的距离分别为 , , ,要在高速公路上E、F之间建一个出口Q,使A、B两城镇到Q的距离之和最短,在图中画出点Q所在位置,并求出这个最短距离. 24. 观察下列一组等式,然后解答后面的问题
24. 观察下列一组等式,然后解答后面的问题,
,
,
(1)、观察以上规律,请写出第 个等式: 为正整数).(2)、利用上面的规律,计算:(3)、请利用上面的规律,比较 与 的大小.25. 一个电器超市购进A、B两种型号的电风扇后进行销售,若一台A种型号的电风扇进价比一台B种型号的电风扇进价多30元,用2000元购进A种型号电风扇的数量是用3400元购进B种型号电风扇的数量的一半.(1)、求每台A种型号电风扇和B种型号的电风扇进价分别是多少?(2)、该超市A种型号电风扇每台售价260元,B种型号电风扇每件售价190元,超市根据市场需求,决定再采购这两种型号的电风扇共30台,若本次购进的两种电风扇全部售出后,总获利不少于1400元,求该超市本次购进A种型号的电风扇至少是多少台?26. (1)、猜想:如图1,已知:在 中, , ,直线m经过点A, 直线m, 直线m,垂足分别为点D、E试猜想 、 、 有怎样的数量关系,请直接写出;(2)、探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在 中, ,D,A、E三点都在直线m上,并且有 (其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由.(3)、解决问题:如图3,F是角平分线上的一点,且 和 均为等边三角形,D、E分别是直线m上A点左右两侧的动点D、E、A互不重合,在运动过程中线段 的长度始终为n,连接 、 ,若 ,试判断 的形状,并说明理由.
(1)、猜想:如图1,已知:在 中, , ,直线m经过点A, 直线m, 直线m,垂足分别为点D、E试猜想 、 、 有怎样的数量关系,请直接写出;(2)、探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在 中, ,D,A、E三点都在直线m上,并且有 (其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由.(3)、解决问题:如图3,F是角平分线上的一点,且 和 均为等边三角形,D、E分别是直线m上A点左右两侧的动点D、E、A互不重合,在运动过程中线段 的长度始终为n,连接 、 ,若 ,试判断 的形状,并说明理由.