河北省廊坊市香河县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-30 类型:期末考试
一、单选题
-
1. 下列代数式中属于分式的是()A、 B、 C、 D、2. 人字梯中间一般会设计一”拉杆”,这样做的道理是( ).
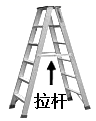 A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性3. 下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )A、
A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性3. 下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )A、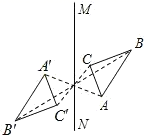 B、
B、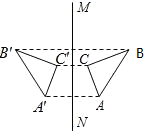 C、
C、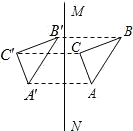 D、
D、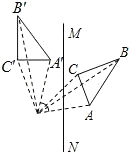 4. 若分式 有意义,则a,b满足的关系是( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、x2-6x+9=(x-3)2 B、x 2-y2=(x-y)2 C、x2-5x+6=(x-1)(x-6) D、6x2+2x=x(6x+2)6. 如图所示,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )个.
4. 若分式 有意义,则a,b满足的关系是( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、x2-6x+9=(x-3)2 B、x 2-y2=(x-y)2 C、x2-5x+6=(x-1)(x-6) D、6x2+2x=x(6x+2)6. 如图所示,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )个.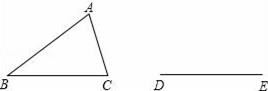 A、2 B、4 C、6 D、87. 如图:若 ,且 ,则EC的长为( )
A、2 B、4 C、6 D、87. 如图:若 ,且 ,则EC的长为( )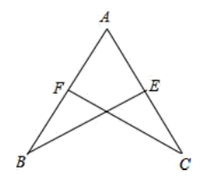 A、2 B、2.5 C、3 D、58. 下列四个图形中,有两个全等的图形,它们是( )
A、2 B、2.5 C、3 D、58. 下列四个图形中,有两个全等的图形,它们是( ) A、①和② B、①和③ C、②和④ D、③和④9. 甲、乙二人做某种零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,若设乙每小时做 个,则可列方程( )A、 B、 C、 D、10. 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A、①和② B、①和③ C、②和④ D、③和④9. 甲、乙二人做某种零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,若设乙每小时做 个,则可列方程( )A、 B、 C、 D、10. 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( ) A、3 B、4 C、5 D、611. 已知 ,则代数式 的值( )A、4 B、9 C、-4 D、-812. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2 , 则S阴影等于…( )
A、3 B、4 C、5 D、611. 已知 ,则代数式 的值( )A、4 B、9 C、-4 D、-812. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2 , 则S阴影等于…( )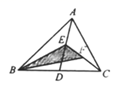 A、2cm2 B、1cm2 C、 cm2 D、 cm213. 如图,在 中, , 和 的平分线交于点E,过点E作 分别交AB、AC于M、N,则 的周长为( )
A、2cm2 B、1cm2 C、 cm2 D、 cm213. 如图,在 中, , 和 的平分线交于点E,过点E作 分别交AB、AC于M、N,则 的周长为( )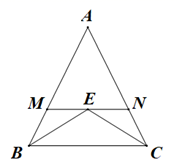 A、12 B、4 C、8 D、不确定14. 如图,AC⊥BC , CD⊥AB , DE⊥BC , 垂足分别为C , D , E , 则下列说法错误的是( )
A、12 B、4 C、8 D、不确定14. 如图,AC⊥BC , CD⊥AB , DE⊥BC , 垂足分别为C , D , E , 则下列说法错误的是( )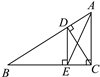 A、AC是△ABC的高 B、DE是△BCD的高 C、DE是△ABE的高 D、AD是△ACD的高15. 如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( )
A、AC是△ABC的高 B、DE是△BCD的高 C、DE是△ABE的高 D、AD是△ACD的高15. 如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( )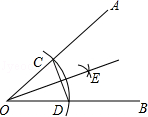 A、射线OE是∠AOB的平分线 B、△COD是等腰三角形 C、C、D两点关于OE所在直线对称 D、O、E两点关于CD所在直线对称
A、射线OE是∠AOB的平分线 B、△COD是等腰三角形 C、C、D两点关于OE所在直线对称 D、O、E两点关于CD所在直线对称二、填空题
-
16. 已知在 中, , ,则边BC的长度的取值范围是 .17. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为度.
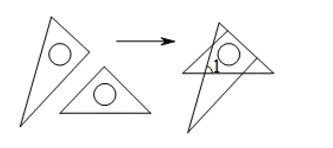 18. 计算: .19. 如图,已知等边△ABC的边长为8cm,∠A=∠B=60°,点D为边BC上一点,且BD=3cm.若点M在线段CA上以2cm/s的速度由点C向点A运动,同时,点N在线段AB上由点A向点B运动,△CDM与△AMN全等,则点N的运动速度是
18. 计算: .19. 如图,已知等边△ABC的边长为8cm,∠A=∠B=60°,点D为边BC上一点,且BD=3cm.若点M在线段CA上以2cm/s的速度由点C向点A运动,同时,点N在线段AB上由点A向点B运动,△CDM与△AMN全等,则点N的运动速度是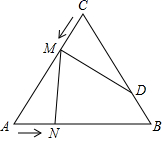 20. 如图,已知等边△ABC的边长为8cm,∠A=∠B=60°,点D为边BC上一点,且BD=3cm.若点M在线段CA上以2cm/s的速度由点C向点A运动,同时,点N在线段AB上由点A向点B运动,△CDM与△AMN全等,则点N的运动速度是
20. 如图,已知等边△ABC的边长为8cm,∠A=∠B=60°,点D为边BC上一点,且BD=3cm.若点M在线段CA上以2cm/s的速度由点C向点A运动,同时,点N在线段AB上由点A向点B运动,△CDM与△AMN全等,则点N的运动速度是
三、解答题
-
21. 计算(1)、(2)、(3)、用简便方法计算:(4)、解分式方程:(5)、22. 先化简,再求值: ,其中 .23. 如图,将 置于直角坐标系中,若点A的坐标为
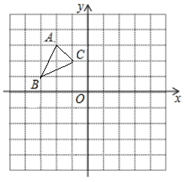 (1)、写出点B和点C的坐标(2)、作 关于x轴对称的图形,并说明对应点的横、纵坐标分别有什么关系?24. 某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了 ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
(1)、写出点B和点C的坐标(2)、作 关于x轴对称的图形,并说明对应点的横、纵坐标分别有什么关系?24. 某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了 ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
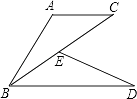
25. 已知:如图,E为BC上一点,AC∥BD,AC=BE,BC=BD.求证:AB=DE.
 26.
26.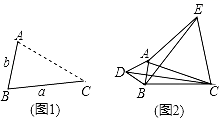 (1)、发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
(1)、发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.①填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)
(2)、应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB、AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
27. 如图(1),AB=4cm , AC⊥AB , BD⊥AB , AC=BD=3cm . 点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).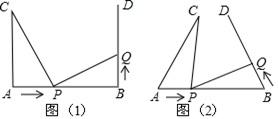 (1)、若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),将图(1)中的“AC⊥AB , BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s , 是否存在实数x , 使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
(1)、若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),将图(1)中的“AC⊥AB , BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s , 是否存在实数x , 使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.