河北省廊坊市霸州市2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-30 类型:期末考试
一、单选题
-
1. 图书馆的标志是浓缩图书馆文化的符号,下列图书馆标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. ( )A、9 B、8 C、 D、3. 在 中,若 , ,则第三边 的取值可能是( )A、3 B、5 C、9 D、104. 下列运算中,正确的是( )A、 B、 C、 D、5. 如图, 等于( )
2. ( )A、9 B、8 C、 D、3. 在 中,若 , ,则第三边 的取值可能是( )A、3 B、5 C、9 D、104. 下列运算中,正确的是( )A、 B、 C、 D、5. 如图, 等于( )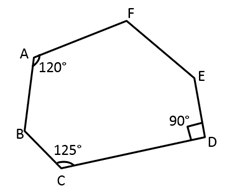 A、360° B、335° C、385° D、405°6. 计算 ,结果用科学记数法表示为( )A、 B、 C、 D、7. 下列因式分解结果正确的是( )A、 B、 C、 D、8. 若经过点 的直线 与 轴平行,则点 关于直线m对称的点的坐标为( )A、 B、 C、 D、9. 若 加上一个单项式就能成为一个完全平方式,则这个单项式不可能是( )A、 B、 C、 D、10. 如图,在折线 中, ,现按如下步骤作图:
A、360° B、335° C、385° D、405°6. 计算 ,结果用科学记数法表示为( )A、 B、 C、 D、7. 下列因式分解结果正确的是( )A、 B、 C、 D、8. 若经过点 的直线 与 轴平行,则点 关于直线m对称的点的坐标为( )A、 B、 C、 D、9. 若 加上一个单项式就能成为一个完全平方式,则这个单项式不可能是( )A、 B、 C、 D、10. 如图,在折线 中, ,现按如下步骤作图: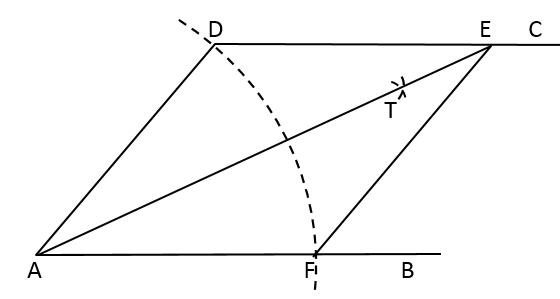 ①以点A为圆心, 长为半径画弧交 于点F;
①以点A为圆心, 长为半径画弧交 于点F;②分别以点D,F为圆心,大于 长为半径画弧,两弧交于点 ;
③作射线 ,交 于点E;
④连接 .
若 ,则 ( )
A、8 B、10 C、12 D、2011. 下列运算中,正确的是( )A、 B、 C、 D、12. 如图,在 中, 于点E, 分别交 , 于点F,D, ,若依据“ ”说明 ,则下列所添条件合理的是( )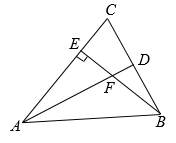 A、 B、 C、 D、13. 如图,在 中, , 平分 ,交 于点D.若 , ,则 的值可能是( )
A、 B、 C、 D、13. 如图,在 中, , 平分 ,交 于点D.若 , ,则 的值可能是( )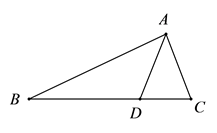 A、7 B、 C、3 D、14. 若关于x的分式方程 的解是非负数,则m的取值范围是( )A、 , B、 且 C、 且 D、
A、7 B、 C、3 D、14. 若关于x的分式方程 的解是非负数,则m的取值范围是( )A、 , B、 且 C、 且 D、二、填空题
-
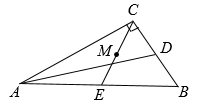
15. 分式 有意义,则x的取值范围是 .16. 若 , ,则 的值为 .17. 如图,在 中, , , , 都是 的中线,点M是 的中点,若 ,则 .
 18. 如图,在 中, , 平分 ,点P,D分别是 和 上的任意一点,设 .
18. 如图,在 中, , 平分 ,点P,D分别是 和 上的任意一点,设 .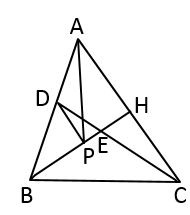 (1)、连接 交 于点E,则m (填表示相等或大小关系的符号);(2)、若 , , ,则m的最小值是 .
(1)、连接 交 于点E,则m (填表示相等或大小关系的符号);(2)、若 , , ,则m的最小值是 .三、解答题
-
19. 计算下列各式.(1)、 ;(2)、 .20. 先化简,再求值: ,其中a是4的平方根.21. 把图1中的三个小长方形与图2中的正方形拼成一个较大的长方形(在图2中画出).根据拼图,在下面的横线上写出一个多项式的因式分解;
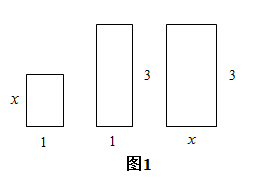
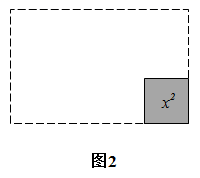 22. 在正方形网格中建立如图所示的直角坐标系,格点(网格线的交点)A,B的坐标分别为 , .利用线段 分别在图1、图2、图3中按要求画出 ,并写出点 的坐标.
22. 在正方形网格中建立如图所示的直角坐标系,格点(网格线的交点)A,B的坐标分别为 , .利用线段 分别在图1、图2、图3中按要求画出 ,并写出点 的坐标.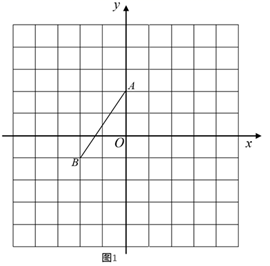
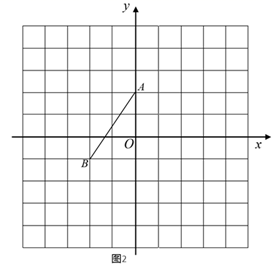
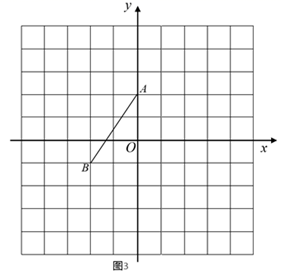 (1)、 的对称轴是y轴;(2)、 的对称轴是过点B且平行于坐标轴的直线,并写出点C的坐标;(3)、 的对称轴是过点B但不平行于坐标轴的直线,且点C落在y轴右侧的格点上.23. 如图,已知在 中,D是 上一点,点F,G都在 上, , ,连接 ,分别延长 , ,且它们相交于点E.
(1)、 的对称轴是y轴;(2)、 的对称轴是过点B且平行于坐标轴的直线,并写出点C的坐标;(3)、 的对称轴是过点B但不平行于坐标轴的直线,且点C落在y轴右侧的格点上.23. 如图,已知在 中,D是 上一点,点F,G都在 上, , ,连接 ,分别延长 , ,且它们相交于点E.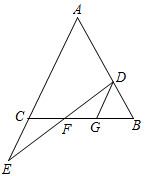 (1)、求证: ;(2)、若 ,点F,G是 上的三等分点, , ,求 的周长.24. 某制药厂生产一种创新型中药,该药对于治疗流感及新冠肺炎都有较好的疗效.该制药厂第一车间原来每天能生产该药品960箱,受疫情影响,曾经停工停产,在复工复产初期,该生产车间仍有6名工人没有报到.已到厂的工人积极生产,原来每天工作8小时,现在每天加班2小时,在每人每小时平均完成的工作量不变的情况下,该车间现在每天能生产该药品840箱.(1)、该制药厂第一车间原来有工人多少人?(2)、就这样加班生产已过10天,该制药车间接到加急任务:将复工后的21000箱药品供应武汉市,制药厂决定从其他制药车间抽调6名技术工人以填补未到岗工人的空缺,并且每天仍然加班生产2小时,那么该车间至少还需要生产多少天才能完成任务?25. 如图1, 是等边三角形,点P为射线 上一动点,连接 ,作 , 交射线 于点E,点O是线段 , 垂直平分线的交点.
(1)、求证: ;(2)、若 ,点F,G是 上的三等分点, , ,求 的周长.24. 某制药厂生产一种创新型中药,该药对于治疗流感及新冠肺炎都有较好的疗效.该制药厂第一车间原来每天能生产该药品960箱,受疫情影响,曾经停工停产,在复工复产初期,该生产车间仍有6名工人没有报到.已到厂的工人积极生产,原来每天工作8小时,现在每天加班2小时,在每人每小时平均完成的工作量不变的情况下,该车间现在每天能生产该药品840箱.(1)、该制药厂第一车间原来有工人多少人?(2)、就这样加班生产已过10天,该制药车间接到加急任务:将复工后的21000箱药品供应武汉市,制药厂决定从其他制药车间抽调6名技术工人以填补未到岗工人的空缺,并且每天仍然加班生产2小时,那么该车间至少还需要生产多少天才能完成任务?25. 如图1, 是等边三角形,点P为射线 上一动点,连接 ,作 , 交射线 于点E,点O是线段 , 垂直平分线的交点.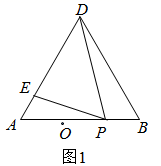 (1)、当点O在 边上时, .(2)、①当点P,B重合时,作 ,交 的垂直平分线于点 ,则 .
(1)、当点O在 边上时, .(2)、①当点P,B重合时,作 ,交 的垂直平分线于点 ,则 .②当点P在线段 上,或 的延长线上时, 的度数是否为定值?若是,请写出这个数,并选择点P在线段 上时,通过计算进行说明;若不是,请说明理由.
(3)、如图2,把等边三角形 沿着 折叠,得到 ,且点A落在点 处,连接 .当 时,证明 平分 ,并在 内确定一点T,使点T到 三边的距离相等(不写作法,只保留作图痕迹).