河北省承德市宽城县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{{(- 2)}^{2}} =$ （）

A、 $- 2$ B、 $2$ C、 $2$ 或 $- 2$ D、4

查看试题解析
2. 下列围形中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算错误的是（）

A、 $\sqrt{2} \times 3 \sqrt{2} = 6$ B、 $\sqrt{\frac{1}{3}} = \frac{\sqrt{3}}{3}$ C、 ${(2 \sqrt{2})}^{2} = 8$ D、 $\sqrt{32} - \sqrt{2} = \sqrt{30}$

查看试题解析
4. 如图，在 $△ A B C$ 中 $A B = A C$ ， $D$ 是 $B C$ 的中点， $∠ B = 36 °$ ，则 $∠ B A D =$ （）.

A、108° B、72° C、54° D、36°

查看试题解析
5. 化简 $\frac{1 - x}{x^{2} - 1}$ 的结果是（）

A、 $- \frac{1}{x + 1}$ B、 $\frac{1}{x - 1}$ C、 $\frac{1}{x + 1}$ D、 $\frac{1}{1 - x}$

查看试题解析
6. 如图，长为 $8 cm$ 的橡皮筋放置在水平面上，固定两端A和B，然后把中点C向上垂直拉升 $3cm$ 至点D，则橡皮筋被拉长了（）

A、 $1cm$ B、 $2cm$ C、 $4 cm$ D、 $5cm$

查看试题解析
7. 用反证法证明“在三角形中，至少有一个内角大于或等于60°”时，应先假设（）

A、在三角形中，三个内角都大于60° B、在三角形中，三个内角都小于60° C、在三角形中，至少有一个内角大于60° D、在三角形中，至少有一个内角小于60°

查看试题解析
8. 如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）

A、∠B=∠D B、BE=DF C、AD=CB D、AD∥BC

查看试题解析
9. 已知a，b为两个连续的整数，且 $a < \sqrt{18} < b$ ，则 $\sqrt{a + b}$ 的值等于（）

A、 $4$ B、 $3$ C、 $5$ D、 $\sqrt{10}$

查看试题解析
10. 下面三个基本作图的作图痕迹．关于三条弧①，②，③，有以下三种说法，

⑴弧①是以点O为圆心，以任意长为半径所作的弧；

⑵弧②是以点A为圆心，以任意长为半径所作的弧；

⑶弧③是以点O为圆心，以大于 $\frac{1}{2}$ DE的长为半径所作的弧．

其中正确说法的个数为（）

A、3个 B、2个 C、1个 D、0个

查看试题解析
11. 如图．从一个大正方形中裁去面积为8m²和18cm²的两个小正方形，则留下的阴影部分的面积为（）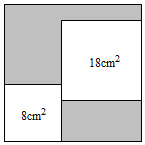

A、 $5 \sqrt{2}$ cm² B、 $12$ cm² C、 $8$ cm² D、 $24$ cm²

查看试题解析
12. 如图，四边形ABCD中，∠A＝90°，AD＝2，连接BD ， BD⊥CD ，垂足是D且∠ADB＝∠C ，点P是边BC上的一动点，则DP的最小值是（　　）

A、1 B、1.5 C、2 D、2.5

查看试题解析
13. 如图，在等边 $Δ A B C$ 中， $B C = 4$ ， $D ， E$ 分别是 $A B$ ， $A C$ 的中点， $E F ⊥ B C$ 于点F，连接 $D F$ ．则 $D F$ 等于（）

A、2 B、3 C、 $\sqrt{7}$ D、 $2 \sqrt{2}$

查看试题解析
14. 若关于x的方程 $\frac{x + m}{x - 4} + \frac{3 m}{4 - x} = 3$ 的解为正数，则m的取值范围是（）．

A、 $m < \frac{9}{2}$ B、 $m > - \frac{9}{4}$ 且 $m \neq - \frac{3}{4}$ C、 $m < 6$ D、 $m < 6$ 且 $m \neq 2$

查看试题解析
15. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ ，垂足为D， $E F$ 垂直平分 $A C$ ，交 $A C$ 于点F，交 $B C$ 于点E， $B D = D E$ ，若 $△ A B C$ 的周长为 $26$ cm， $A F = 5$ cm，则 $D C =$ （）

A、 $8$ cm B、 $7$ cm C、 $10$ cm D、 $9$ cm

查看试题解析
16. 如图．已知正方形 $A B C D$ 的边长为 $12$ ． $B E = E C$ ，将正方形的边 $C D$ 沿 $D E$ 折叠到 $D F$ ，延长 $E F$ 交 $A B$ 于G，连接 $D G$ ．现有如下 $3$ 个结论；① $A G + E C = G E$ ；② $∠ G D E = 45 °$ ；③ $△ B G E$ 的周长是 $24$ ．其中正确的个数为（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析

二、填空题

17. 当代数式 $\frac{\sqrt{4 - x}}{x^{2} - 1}$ 有意义时，x应满足的条件．

查看试题解析
18. 若正实数x的两个平方根分别为 $2 a + 1$ 和 $3 a - 4$ ，实数y的立方根为 $- a$ ，则 $x + y$ 的值为．

查看试题解析
19. 阅读下列内容：设a，b，c是一个三角形的三条边的长，且a最大，我们可以利用a，b，c之间的关系来判断这个三角形的形状：①若 $a^{2} = b^{2} + c^{2}$ ，则该三角形是直角三角形；②若 $a^{2} > b^{2} + c^{2}$ ，则该三角形是钝角三角形；③若 $a^{2} < b^{2} + c^{2}$ ，则该三角形是锐角三角形．例如：若一个三角形的三边长分别是 $4$ ， $5$ ， $6$ ，则最长边是 $6$ ， $6^{2} = 36 < 4^{2} + 5^{2}$ ，故由③可知该三角形是锐角三角形．

(1)、若一个三角形的三边长分别是 $7$ ， $8$ ， $9$ ，则该三角形是；

(2)、若一个三角形的三边长分别是 $5$ ， $12$ ，x，且这个三角形是直角三角形，则x的值为；

(3)、带一个三角形的三边长 $a = \sqrt{x^{2} + 3 z^{2}}$ ， $b = \sqrt{x - y^{2}}$ ， $c = \sqrt{2 y - \frac{9}{2}}$ ，其中a是最长边长，则该三角形是三角形．

查看试题解析

三、解答题

20. 先化简，再求值．

(1)、 $(\frac{x + 1}{x - 2} - 1) \div \frac{x^{2} - 2 x}{x^{2} - 4 x + 4}$ ，其中 $x$ 是9的平方根；

(2)、 $(\frac{2 a^{2} - 2 a}{a^{2} - 2 a + 1} - 1) \div \frac{a^{2} + a}{a^{2} - 1}$ ，然后从－1，0，1，2中选一个合适的数作为 $a$ 的值代入求值．

查看试题解析
21. 如图，小明家在一条东西走向的公路 $M N$ 北侧 $200$ 米的点A处，小红家位于小明家北 $500$ 米（ $A C = 500$ 米）、东 $1200$ 米（ $B C = 1200$ 米）点B处．

(1)、求小明家离小红家的距离 $A B$ ；

(2)、现要在公路 $M N$ 上的点P处建一个快递驿站，使 $P A + P B$ 最小，请确定点P的位置，并求 $P A + P B$ 的最小值．

查看试题解析
22. 如图．已知点D和点B在线段 $A E$ 上，且 $A D = B E$ ，点C和点F在 $A E$ 的同侧， $∠ A = ∠ E$ ， $A C = E F$ ， $D F$ 和 $B C$ 相交于点 $H$ ．

(1)、求证： $B C = D F$ ；

(2)、当 $∠ C H D = 120 °$ 时，猜想 $△ H D B$ 的形状，并说明理由．

查看试题解析
23. 有一个数值转换器，程序如图所示，按要求完成下列各小题．

(1)、当输入的x值为 $\sqrt{3} - 2$ 时，求输出的结果；

(2)、当输入的x值为 $\sqrt{3} - 1$ 时，求输出的结果．

查看试题解析
24. 新冠肺炎疫情防控期间，学校为做好预防性消毒工作，开学初购进 $A$ 、 $B$ 两种消毒液，其中 $A$ 消毒液的单价比 $B$ 消毒液的单价多40元，用3200元购买 $B$ 消毒液的数量是用2400元购买 $A$ 消毒液数量的2倍．

(1)、求两种消毒液的单价；

(2)、学校准备用不多于6800元的资金购买 $A$ 、 $B$ 两种消毒液共70桶，问最多购买 $A$ 消毒液多少桶？

查看试题解析
25. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，直线 $M N$ 经过点C，且 $A D ⊥ M N$ 于点D， $B E ⊥ M N$ 于点E．

(1)、当直线MN绕点C旋转到图1的位置时，求证：① $△ A D C ≌ △ C E B$ ；② $D E = A D + B E$ ；

(2)、当直线 $M N$ 绕点C旋转到如图2所示的位置时，求证： $D E = A D - B E$ ；

(3)、当直线 $M N$ 绕点C旋转到如图3所示的位置时，试问 $D E$ ， $A D$ ， $B E$ 具有怎样的数量关系？请直接写出这个等量关系，不需要证明．

查看试题解析
26. 在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 8$ ， $A B = 10$ ．

(1)、如图1，求点C到边 $A B$ 的距离；

(2)、点M是 $A B$ 上一动点．
①如图2．过点M作 $M N ⊥ A B$ 交 $A C$ 于点N，当 $M N = C N$ 时，求 $A M$ 的长；

②如图3，连接 $C M$ ，当 $A M$ 为何值时， $△ B C M$ 为等腰三角形？

查看试题解析