河北省承德市丰宁满族自治县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 使分式 $\frac{1}{x - 2}$ 有意义时x的取值范围为（）

A、 $x > 0$ B、 $x \neq - 2$ C、 $x \neq 2$ D、任意实数

查看试题解析
2. 等腰三角形的顶角是100°，则它的底角度数是（）

A、80° B、40° C、30° D、20°

查看试题解析
3. 下列计算正确的是（）

A、 ${(a^{2} b)}^{2} = a^{2} b^{2}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 ${(- 3 x y^{2})}^{2} = 9 x^{2} y^{4}$ D、 ${(- m)}^{7} \div {(- m)}^{2} = m^{5}$

查看试题解析
4. KN95型口罩可以保护在颗粒物浓度很高的空间中工作的人不被颗粒物侵害，也可以帮助人们预防传染病．“KN95”表示此类型的口罩能过滤空气中95%的粒径约为0.0000003m的非油性颗粒．其中，0.0000003用科学记数法表示为（）

A、3×10^﹣6 B、3×10^﹣7 C、0.3×10^﹣6 D、0.3×10^﹣7

查看试题解析
5. 下列长度的三条小木棒能构成三角形的是（　　）

A、1cm 2cm 3cm B、2cm 4cm 6cm C、3cm 4cm 8cm D、6cm 8cm 10cm

查看试题解析
6. 把分式方程 $\frac{2}{x - 1} = \frac{5}{x + 1}$ 转化为一元一次方程时，方程两边需同乘以（）

A、 $x - 1$ B、 $x + 1$ C、 $x^{2} - 1$ D、 $x^{2} + x$

查看试题解析
7. 下列各式从左到右的变形是因式分解的是（）

A、 $6 x + 9 y + 3 = 3 (2 x + 3 y)$ B、 $x^{2} - 1 = {(x - 1)}^{2}$ C、 $(x + y) (x - y) = x^{2} - y^{2}$ D、 $2 x^{2} - 2 = 2 (x - 1) (x + 1)$

查看试题解析
8. 如果一个多边形的内角和等于900°，这个多边形是（　　）

A、四边形 B、五边形 C、六边形 D、七边形

查看试题解析
9. 如图， $△ A B C ≅ △ C D A$ ， $∠ B A C = ∠ D C A$ ，则 $B C$ 的对应边是（）

A、 $C D$ B、 $C A$ C、 $D A$ D、 $A B$

查看试题解析
10. 已知 $a - b = 2$ ， $a b = 3$ ，则 $a^{2} + b^{2}$ 的值是（　　）

A、1 B、6 C、10 D、11

查看试题解析
11. 已知点M（3，a）和N（b ， 4）关于x轴对称，则 ${(a + b)}^{2021}$ 的值为（）

A、1 B、–1 C、72021 D、–72021

查看试题解析
12. 如图，在Rt△ABC中，∠C ＝ 90°，∠B ＝30°，D是BC上一点，DE⊥AB于点E ，且DE＝DC ，则∠CAD的度数为（）

A、15° B、20° C、25° D、30°

查看试题解析
13. 若 $(x - a) (x - 5)$ 的展开式中不含有x的一次项，则a的值为（）

A、0 B、5 C、 $- 5$ D、5或 $- 5$

查看试题解析
14. 某厂接到加工720件衣服的订单，预计每天做48件，正好按时完成，后因客户要求提前5天交货，设每天应多做x件，则x应满足的方程为（）

A、 $\frac{720}{48 + x} - \frac{720}{48} = 5$ B、 $\frac{720}{48} + 5 = \frac{720}{48 + x}$ C、 $\frac{720}{48} - \frac{720}{x} = 5$ D、 $\frac{720}{48} - \frac{720}{48 + x} = 5$

查看试题解析
15. 如图，△ABC ， AB＝10cm，BC＝7 cm，AC＝6 cm，沿过点 B 的直线折叠这个三角形，使顶点C 落在 AB 边上的点E 处，折痕为BD ，则△AED 的周长为（）

A、6cm B、7cm C、9cm D、10cm

查看试题解析
16. 如果 $a - b = - 2$ ，那么代数式 $(\frac{a^{2} + b^{2}}{a} - 2 b) \cdot \frac{a}{a - b}$ 的值是（　　）

A、2 B、–2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析

二、填空题

17. 若分式 $\frac{| y | - 2}{2 - y}$ 的值为零，则y＝．

查看试题解析
18. 如图， $△ A B C ≌ △ D E F$ ，BE=4，AE=1，则DE的长是．

查看试题解析
19. 已知 ${(a^{n} b^{m + 2})}^{3} = a^{6} b^{15}$ ，则 $m^{n} =$ ．

查看试题解析
20. 在平面直角坐标系 $x O y$ 中，点A的坐标为 $(0 ， 3)$ ，点B与点A关于x轴对称，点C在x轴上，若三角形ABC为等腰直角三角形，则点C的坐标为．

查看试题解析

三、解答题

21. 先化简，再求值

(1)、 $(2 a - 1) (2 a + 1) - {(2 a + 1)}^{2}$ ，其中 $a = - \frac{3}{4}$ ．

(2)、 $(\frac{1}{x + 1} - \frac{1}{x - 1}) \div \frac{2}{x - 1}$ ，其中 $x = - 2$ ．

查看试题解析
22. 如图所示的坐标系中，△ABC的三个顶点的坐标依次为A（﹣1，2），B（﹣4，1），C（﹣2，﹣2）.

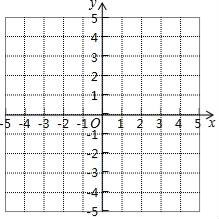(1)、请在这个坐标系中作出△ABC关于y轴对称的△A₁B₁C₁.

(2)、分别写出点A₁、B₁、C₁的坐标.

(3)、求△A₁B₁C₁的面积.

查看试题解析
23. 阅读下面的材料并解答后面的问题：
在学了整式的乘法公式后，小明问：能求出 $x^{2} + 4 x + 3$ 的最小值吗？如果能，其最小值是多少？

小丽：能．求解过程如下：因为 $x^{2} + 4 x + 3 = x^{2} + 4 x + 4 - 4 + 3 = {(x + 2)}^{2} - 1$ ，

因为 ${(x + 2)}^{2} \geq 0$ ，所以 $x^{2} + 4 x + 3$ 的最小值是 $- 1$ ．

问题：

(1)、小丽的求解过程正确吗？

(2)、你能否求出 $x^{2} - 8 x + 5$ 的最小值？如果能，写出你的求解过程；

(3)、求 $- x^{2} + 6 x - 5$ 的最大值．

查看试题解析
24. 如图，AB∥CD ， BC分别交AB ， CD于点B ， C ．

(1)、尺规作图：作 $∠ B C D$ 的平分线CE交AB于点E（不写作法，只保留作图痕迹）；

(2)、在（1）的图中，证明BC＝BE ．

查看试题解析
25. 甲、乙两个施工队共同完成某区域绿化改造工程，乙队先单独做3天后，再由两队合作7天完成全部工程．已知乙队单独完成此项工程所需天数是甲队单独完成此项工程所需天数的2倍，求甲、乙两个施工队单独完成此项工程各需多少天？

查看试题解析
26. 如图1，在△ABC中，∠ACB=90°，AC= $\frac{1}{2}$ BC ，点D为BC的中点，AB =DE ， BE∥AC ．

(1)、求证：△ABC≌△DEB；

(2)、连接AD、AE、CE ，如图2．
①求证：CE是∠ACB的角平分线；

②请判断△ABE是什么特殊形状的三角形，并说明理由．

查看试题解析