河北省沧州市2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-30 类型:期末考试
一、单选题
-
1. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯是现在世界上最薄的纳米材料,其理论厚度应是0.0000034 m,用科学记数法表示0.0000034是( )A、0.34×10-5 B、3.4×106 C、3.4×10-5 D、3.4×10-63. 下列运算正确的是( )A、 B、 C、 D、4. 一边长为3,另一边长为6的等腰三角形的周长是( )A、12 B、15 C、12或15 D、95. 若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )A、a=5,b=﹣6 B、a=5,b=6 C、a=1,b=6 D、a=1,b=﹣66. 一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形7. 如图, AD是 的中线,E、F分别是AD和AD延长线上的点,且 ,连结BF、CE . 下列说法:①CE=BF②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
2. 随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯是现在世界上最薄的纳米材料,其理论厚度应是0.0000034 m,用科学记数法表示0.0000034是( )A、0.34×10-5 B、3.4×106 C、3.4×10-5 D、3.4×10-63. 下列运算正确的是( )A、 B、 C、 D、4. 一边长为3,另一边长为6的等腰三角形的周长是( )A、12 B、15 C、12或15 D、95. 若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )A、a=5,b=﹣6 B、a=5,b=6 C、a=1,b=6 D、a=1,b=﹣66. 一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形7. 如图, AD是 的中线,E、F分别是AD和AD延长线上的点,且 ,连结BF、CE . 下列说法:①CE=BF②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )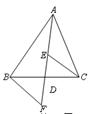 A、1个 B、2个 C、3个 D、4个8. 如图, ,点 为 上一点,以点 为圆心、任意长为半径画弧,交 于点 ,交 于点 .再分别以点 , 为圆心、大于 的长为半径画弧,两弧交于点 .作射线 ,在 上取点 ,连接 ,过点 作 ,垂足为点 .若 ,则 的长可能为
A、1个 B、2个 C、3个 D、4个8. 如图, ,点 为 上一点,以点 为圆心、任意长为半径画弧,交 于点 ,交 于点 .再分别以点 , 为圆心、大于 的长为半径画弧,两弧交于点 .作射线 ,在 上取点 ,连接 ,过点 作 ,垂足为点 .若 ,则 的长可能为 A、1 B、2 C、 D、9. 已知 ,则 的值是( )A、 B、 C、2 D、-210. 一个凸多边形的每一个内角都等于140°,则这个多边形的对角线的条数是( )A、9条 B、54条 C、27条 D、6条11. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =12. 如图,一正方形的边长增加 ,它的面积就增加 ,这个正方形的边长为( )
A、1 B、2 C、 D、9. 已知 ,则 的值是( )A、 B、 C、2 D、-210. 一个凸多边形的每一个内角都等于140°,则这个多边形的对角线的条数是( )A、9条 B、54条 C、27条 D、6条11. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =12. 如图,一正方形的边长增加 ,它的面积就增加 ,这个正方形的边长为( ) A、 B、 C、 D、13. 若 、 、 为一个三角形的三条边,则 的值( )A、一定为正数 B、一定为负数 C、可能为0 D、可能为正数,也可能为负数14. 如图,Rt△ACB中,∠ACB=90°,∠A=60°,CD、CE分别是△ABC的高和中线,下列说法错误的是( )
A、 B、 C、 D、13. 若 、 、 为一个三角形的三条边,则 的值( )A、一定为正数 B、一定为负数 C、可能为0 D、可能为正数,也可能为负数14. 如图,Rt△ACB中,∠ACB=90°,∠A=60°,CD、CE分别是△ABC的高和中线,下列说法错误的是( ) A、AD = AB B、S△CEB = S△ACE C、AC、BC的垂直平分线都经过E D、图中只有一个等腰三角形15. 如图, 中, 垂直平分 ,点P为直线 上的任一点,则 周长的最小值是( )
A、AD = AB B、S△CEB = S△ACE C、AC、BC的垂直平分线都经过E D、图中只有一个等腰三角形15. 如图, 中, 垂直平分 ,点P为直线 上的任一点,则 周长的最小值是( ) A、10 B、14 C、15 D、1916. 如图,平面直角坐标系中,O是坐标原点,点A(3,2),点P(m,0),若△POA是等腰三角形,则m可取的值最多有( )
A、10 B、14 C、15 D、1916. 如图,平面直角坐标系中,O是坐标原点,点A(3,2),点P(m,0),若△POA是等腰三角形,则m可取的值最多有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
17.(1)、若 ,则 .(2)、若 ,则x的值是 .18. 用4个全等的正八边形拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图1,用n个全等的正六边形按这种方式拼接,如图2,若围成一圈后中间也形成一个正多边形,则n的值为 .
 19. 如图 1,△ABC 中, AD 是∠BAC 的平分线,若 AB=AC+CD,那么∠ACB与∠ABC 有怎样的数量关系?小明通过观察分析,形成了如下解题思路:
19. 如图 1,△ABC 中, AD 是∠BAC 的平分线,若 AB=AC+CD,那么∠ACB与∠ABC 有怎样的数量关系?小明通过观察分析,形成了如下解题思路:
如图 2,延长 AC 到 E,使 CE=CD,连接 DE.由 AB=AC+CD,可得 AE=AB.又因为AD是∠BAC 的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB 与∠ABC 的数量关系.
(1)、判定△ABD 与△AED 全等的依据是;(2)、∠ACB 与∠ABC 的数量关系为: .三、解答题
-
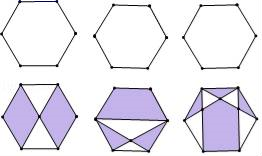
20. 如图,有六个正六边形,在每个正六边形里有六个顶点,要求用两个顶点连线(即正六边形的对角线)将正六方形分成若干块,相邻的两块用黑白两色分开.最后形成轴对称图形,图中已画出三个,请你继续画出三个不同的轴对称图形(至少用两条对角线)
 21.(1)、分解因式(2)、解分式方程:(3)、先化简: ,然后a在 , ,1,2五个数中选一个你认为合适的数代入求值.22. 如图,已知AD,AF分别是两个钝角△ABC 和△ABE的高,如果 AD=AF,AC=AE.求证:BC=BE.
21.(1)、分解因式(2)、解分式方程:(3)、先化简: ,然后a在 , ,1,2五个数中选一个你认为合适的数代入求值.22. 如图,已知AD,AF分别是两个钝角△ABC 和△ABE的高,如果 AD=AF,AC=AE.求证:BC=BE. 23. 如图,在 中, , 的垂直平分线交 于N,交 于M.
23. 如图,在 中, , 的垂直平分线交 于N,交 于M. (1)、若 ,则 的度数是;若 ,则 的度数是;(2)、若 ,你认为 与 怎样的数量关系?说出你的理由;(3)、连接 ,若 , 的周长是 .求 的长;24.(1)、分解下列因式,将结果直接写在横线上:
(1)、若 ,则 的度数是;若 ,则 的度数是;(2)、若 ,你认为 与 怎样的数量关系?说出你的理由;(3)、连接 ,若 , 的周长是 .求 的长;24.(1)、分解下列因式,将结果直接写在横线上:;
;
;
(2)、观察以上三个多项式的系数,我们发现:,
,
;
①猜想结论:若多项式 是完全平方式,则系数a,b,c一定存在某种关系;请你用式子表示a,b,c之间的关系;
②验证结论:请你写出一个完全平方式(不同于题中所出现的完全平方式),并验证①中的结论;
③解决问题:若多项式 是一个完全平方式,求m的值.
25. 某超市在2017年“双11”,销售一批用16800元购进的中老年人保暖内衣,发现供不应求.为了备战“双12”,积极参与支付宝扫码领红包活动,超市又用36400元购进了第二批这种保暖内衣,所购数量是第一批购进量的2倍,但单价贵了10元. (1)、该超市购进的第一批保暖内衣是多少件?(2)、两批保暖内衣按相同的标价销售,最后剩下的50件按六折优惠卖出,两批保暖内衣全部售完后利润没有低于进价的20%(不考虑其他因素),请计算每件保暖内衣的标价至少是多少元?26.
(1)、该超市购进的第一批保暖内衣是多少件?(2)、两批保暖内衣按相同的标价销售,最后剩下的50件按六折优惠卖出,两批保暖内衣全部售完后利润没有低于进价的20%(不考虑其他因素),请计算每件保暖内衣的标价至少是多少元?26. (1)、如图①,已知: 中, , ,直线m经过点A, 于D, 于E,请探索 、 、 三条线段之间的数量关系,直接写出结论;(2)、拓展:如图2,将(1)中的条件改为: 中, ,D、A、E三点都在直线m上,并且 , 为任意锐角或钝角,请问(1)中结论是否还成立?如成立,请证明;若不成立,请说明理由;(3)、应用:如图③,在 中, 是钝角, , , ,直线m与 的延长线交于点F,若 , 的面积是16,求 与 的面积之和.
(1)、如图①,已知: 中, , ,直线m经过点A, 于D, 于E,请探索 、 、 三条线段之间的数量关系,直接写出结论;(2)、拓展:如图2,将(1)中的条件改为: 中, ,D、A、E三点都在直线m上,并且 , 为任意锐角或钝角,请问(1)中结论是否还成立?如成立,请证明;若不成立,请说明理由;(3)、应用:如图③,在 中, 是钝角, , , ,直线m与 的延长线交于点F,若 , 的面积是16,求 与 的面积之和.