北京市顺义区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 若式子 $\frac{\sqrt{x - 2}}{x - 3}$ 有意义，则x的取值范围为(　　)

A、x≥2 B、x≠3 C、x＞2或x≠3 D、x≥2且x≠3

查看试题解析
2. 在下列四个图案中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 实数 $- 2$ ，0.3， $\frac{22}{7}$ ， $\sqrt{2}$ ， $- π$ 中，无理数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
4. 若 $m = \sqrt{10} - 1$ ，则估计m的值所在的范围是（）

A、 $0 < m < 1$ B、 $1 < m < 2$ C、 $2 < m < 3$ D、 $3 < m < 4$

查看试题解析
5. 下列事件中，是必然事件的是（）

A、任意买一张电影票，座位号是2的倍数 B、车辆随机到达一个路口，遇到红灯 C、13个人中至少有两个人生肖相同 D、明天一定会下雨

查看试题解析
6. 如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）

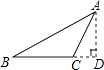A、 B、 C、 D、

查看试题解析
7. 化简 $\frac{a^{2} b - a b^{2}}{b - a}$ 结果正确的是（）

A、 $a b$ B、 $- a b$ C、 $a^{2} - b^{2}$ D、 $b^{2} - a^{2}$

查看试题解析
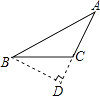8. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{2} = 6$ C、 $\sqrt{8} \div \sqrt{2} = 4$ D、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$

查看试题解析
9. 用长分别为3cm，4cm，7cm的三条线段围成三角形的事件是（）

A、随机事件 B、必然事件 C、不可能事件 D、以上都不是

查看试题解析
10. 如图，已知 $△ A B C$ 中， $∠ A B C = 45 °$ ，F是高 $A D$ 和 $B E$ 的交点， $A C = \sqrt{5}$ ， $B D = 2$ ，则线段 $D F$ 的长度为（）

A、 $2 \sqrt{2}$ B、2 C、 $\sqrt{3}$ D、1

查看试题解析

二、填空题

11. 27的立方根为．

查看试题解析
12. 若代数式 $\frac{x - 2}{x + 3}$ 的值等于零，则实数x的值是．

查看试题解析
13. 如图，小明用直尺和圆规作一个角等于已知角，则说明 $∠ A^{'} O^{'} B^{'} = ∠ A O B$ 的依据是．

查看试题解析
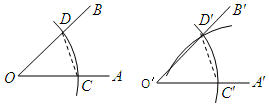14. 若 $\sqrt{{(1 - a)}^{2}} = a - 1$ ，则实数a的取值范围是．

查看试题解析
15. 命题“到线段两个端点距离相等的点在这条线段的垂直平分线上”，它的逆命题是．

查看试题解析
16. 如图，在 $Δ A B C$ 中， $A B = A C ， B D ⊥ A C$ 于点 $D ， ∠ A = 50 °$ ，则 $∠ D B C$ 的度数为．

查看试题解析
17. 如图，已知∠AOB=30°，P是∠AOB平分线上一点，CP∥OB，交OA于点C，PD⊥OB，垂足为点D，且PC=4，则PD等于．

查看试题解析
18. 若实数a，b在数轴上的位置如图，且|a|>[b|，则化简 $\sqrt{a^{2}} - | a + b |$ 的结果为

查看试题解析
19. 如图， $△ A B C$ 是等边三角形， $A E = B D$ ， $A D$ 与 $C E$ 交于点F，则 $∠ C F D$ 的度数是．

查看试题解析
20. 已知 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 2 cm ， A C + B C = \sqrt{6} cm$ ，则 $△ A B C$ 的面积为．

查看试题解析

三、解答题

21. 计算： ${(\sqrt{3} - \sqrt{2})}^{2} - \sqrt{2} (\sqrt{3} - \sqrt{2})$ ．

查看试题解析
22. 计算： $\sqrt{24} \div \sqrt{3} + 2 \sqrt{\frac{1}{2}}$

查看试题解析
23. 某学生化简分式 $\frac{1}{x + 1} + \frac{2}{x^{2} - 1}$ 出现了不符合题意，解答过程如下：
原式= $\frac{1}{(x + 1) (x - 1)} + \frac{2}{(x + 1) (x - 1)}$ （第一步）

= $\frac{1 + 2}{(x + 1) (x - 1)}$ （第二步）

= $\frac{3}{x^{2} - 1}$ ．（第三步）

(1)、该学生解答过程是从第步开始出错的，其错误原因是；

(2)、请写出此题正确的解答过程．

查看试题解析
24. 先化简，再求值： $(\frac{1}{a - 3} + \frac{1}{a + 3}) \div \frac{2 a}{a^{2} - 6 a + 9}$ ，其中 $a = - 2$ ．

查看试题解析
25. 一个不透明的口袋里有5个除颜色外都相同的球，其中有2个红球，3个黄球．

(1)、若从中随意摸出一个球，求摸出红球的可能性；

(2)、若要使从中随意摸出一个球是红球的可能性为 $\frac{2}{3}$ ，求袋子中需再加入几个红球？

查看试题解析
26. 解方程： $\frac{2 x}{x - 2}$ =1﹣ $\frac{1}{2 - x}$ .

查看试题解析
27. 如图，点 $C$ 、 $E$ 在线段 $B F$ 上， $B E = C F$ ， $A B / / D E$ ， $∠ A = ∠ D$ .
求证： $A C = D F$ .

查看试题解析
28. 如图，△ $A B C$ 中， $∠ A C B = 90 °$ ，D为 $A B$ 的中点，连接 $C D$ ，过点B作 $C D$ 的平行线 $E F$ ，求证： $B C$ 平分 $∠ A B F$ ．

查看试题解析
29. 如图，在边长为1个单位长度的小正方形组成的网格中，按要求作图．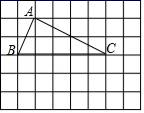

⑴利用尺规作图在AC边上找一点D，使点D到AB、BC的距离相等．（不写作法，保留作图痕迹）

⑵在网格中，△ABC的下方，直接画出△EBC，使△EBC与△ABC全等．

查看试题解析
30. 为改善生态环境，防止水土流失，某村计划在荒坡上种1000棵树．由于青年志愿者的支援，每天比原计划多种25%，结果提前5天完成任务，原计划每天种多少棵树？

查看试题解析
31. 小明将一副三角板按如图所示摆放在一起，发现只要知道其中一边的长就可以求出其他各边的长，若已知CD=2，求AC的长．

查看试题解析
32. 已知：如图， $A C / / B D$ ， $A E$ ， $B E$ 分别平分 $∠ C A B$ 和 $∠ A B D$ ，点E在 $C D$ 上．用等式表示线段 $A B$ 、 $A C$ 、 $B D$ 三者之间的数量关系，并证明．

查看试题解析