北京市海淀区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $A (2 ， 3)$ ，则k的值为（）

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
2. 围棋起源于中国，古代称之为“弈”，至今已有 $4000$ 多年的历史． $2017$ 年 $5$ 月，世界围棋冠军柯洁与人工智能机器人 $AlphaGo$ 进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（）

A、 B、 C、 D、

查看试题解析
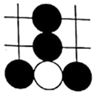3. 不透明袋子中有 $1$ 个红球和 $2$ 个绿球，这些球除颜色外无其他差别．从袋子中随机取出 $1$ 个球，恰好是红球的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $1$

查看试题解析
4. 如图， $△ A B C$ 中，点D，E分别在边 $A B$ ， $A C$ 的反向延长线上，且 $D E // B C$ ．若 $A E = 2$ ， $A C = 4$ ， $A D = 3$ ，则 $A B$ 为（）

A、9 B、6 C、3 D、 $\frac{3}{2}$

查看试题解析
5. 在下列方程中，有一个方程有两个实数根，且它们互为相反数，这个方程是（）

A、 $x - 1 = 0$ B、 $x^{2} + x = 0$ C、 $x^{2} - 1 = 0$ D、 $x^{2} + 1 = 0$

查看试题解析
6. 如图， $⊙ O$ 的内接正六边形 $A B C D E F$ 的边长为 $1$ ，则 $\overset{⌢}{B C}$ 的长为（）

A、 $\frac{1}{4} π$ B、 $\frac{1}{3} π$ C、 $\frac{2}{3} π$ D、 $π$

查看试题解析
7. 已知二次函数 $y = a x^{2} + b x + c$ 的部分图象如图所示，则使得函数值 $y$ 大于 $2$ 的自变量 $x$ 的取值可以是（）

A、-4 B、-2 C、0 D、2

查看试题解析
8. 下列选项中，能够被半径为1的圆及其内部所覆盖的图形是（）

A、长度为 $\sqrt{5}$ 的线段 B、斜边为3的直角三角形 C、面积为4的菱形 D、半径为 $\sqrt{2}$ ，圆心角为 $90 °$ 的扇形

查看试题解析

二、填空题

9. 写出一个二次函数，使得它有最小值，这个二次函数的解析式可以是．

查看试题解析
10. 若点 $(1 ， a)$ ， $(2 ， b)$ 都在反比例函数 $y = \frac{4}{x}$ 的图象上，则a，b的大小关系是：ab．（填“ $>$ ”、“ $=$ ”或“ $<$ ”）

查看试题解析
11. 如图， $△ A B C$ 为等腰三角形，O是底边 $B C$ 的中点，若腰 $A B$ 与 $⊙ O$ 相切，则 $A C$ 与 $⊙ O$ 的位置关系为．（填“相交”、“相切”或“相离”）

查看试题解析
12. 关于x的一元二次方程 $x^{2} - 3 x + k = 0$ 有一个根为1，则k的值等于．

查看试题解析

13. 某城市启动“城市森林”绿化工程，林业部门要考察某种树苗在一定条件下的移植成活率．在同样条件下，对这种树苗进行大量移植，并统计成活情况，数据如下表所示：

移植总数	$10$	$270$	$400$	$750$	$1500$	$3500$	$7000$	$9000$	$14000$
成活数量	$8$	$235$	$369$	$662$	$1335$	$3203$	$6335$	$8073$	$12628$
成活频率	$0.800$	$0.870$	$0.923$	$0.883$	$0.890$	$0.915$	$0.905$	$0.897$	$0.902$

估计树苗移植成活的概率是．（结果保留小数点后一位）

查看试题解析

14. 如图，在测量旗杆高度的数学活动中，某同学在脚下放了一面镜子，然后向后退，直到他刚好在镜子中看到旗杆的顶部．若眼睛距离地面 $A B = 1.5 m$ ，同时量得 $B C = 2 m$ ， $C D = 12 m$ ，则旗杆高度 $D E =$ $m$ ．

查看试题解析
15. 如图，在 $Rt △ A B C$ 中， $∠ A B C = 90 °$ ， $A B = B C = 3$ ，点D在 $A C$ 上，且 $A D = 2$ ，将点D绕着点A顺时针方向旋转，使得点D的对应点E恰好落在 $A B$ 边上，则旋转角的度数为， $C E$ 的长为．

查看试题解析
16. 已知双曲线 $y = - \frac{3}{x}$ 与直线 $y = k x + b$ 交于点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ．

(1)、若 $x_{1} + x_{2} = 0$ ，则 $y_{1} + y_{2} =$ ；

(2)、若 $x_{1} + x_{2} > 0$ 时， $y_{1} + y_{2} > 0$ ，则k0，b0．（填“>”，“=”或“<”）

查看试题解析
17. 如图1是博物馆展出的古代车轮实物，《周礼·考工记》记载：“……故兵车之轮六尺有六寸，田车之轮六尺有三寸……”据此，我们可以通过计算车轮的半径来验证车轮类型，请将以下推理过程补充完整．

如图 $2$ 所示，在车轮上取A、B两点，设 $\overset{⌢}{A B}$ 所在圆的圆心为O，半径为 $r cm$ ．作弦 $A B$ 的垂线 $O C$ ，D为垂足，则D是 $A B$ 的中点．其推理依据是：．经测量： $A B = 90 cm$ ， $C D = 15 cm$ ，则 $A D =$ $cm$ ；用含 $r$ 的代数式表示 $O D$ ， $O D =$ $cm$ ．在 $Rt △ O A D$ 中，由勾股定理可列出关于 $r$ 的方程： $r^{2} =$ ，解得 $r = 75$ ．通过单位换算，得到车轮直径约为六尺六寸，可验证此车轮为兵车之轮．

查看试题解析

三、解答题

18. 解方程：x²﹣4x+3=0；

查看试题解析
19. 如图，在 $Rt △ A B C$ 和 $Rt △ A C D$ 中， $∠ B = ∠ A C D = 90 °$ ， $A C$ 平分 $∠ B A D$ ．

(1)、证明： $△ A B C ∽ △ A C D$ ；

(2)、若 $A B = 4$ ， $A C = 5$ ，求 $B C$ 和 $C D$ 的长．

查看试题解析
20. 文具店购进了20盒“2B铅笔”，但在销售过程中发现其中混入了若干“HB铅笔”，店员进行统计后发现每盒铅笔中最多混入了2支“HB铅笔”，具体数据如下表：

混入“HB”铅笔数

0

1

2

盒数

6

m

n

(1)、用等式写出m、n满足的关系式；

(2)、从20盒中任意选取1盒；
①“盒子中没有混入HB铅笔”是事件；

②若“盒中混入1支HB铅笔”的概率为0.25，求m、n的值．

查看试题解析
21. 如图，在平面直角坐标系 $x O y$ 中，线段 $A B$ 两个端点的坐标分别为 $A (1 ， 2)$ ， $B (4 ， 2)$ ，以点O为位似中心，相似比为 $2$ ，在第一象限内将线段 $A B$ 放大得到线段 $C D$ ．已知点B在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上．

(1)、求反比例函数的解析式，并画出图象；

(2)、判断点C是否在此函数图象上；

(3)、点M为直线 $C D$ 上一动点，过M作x轴的垂线，与反比例函数的图象交于点N．若 $M N \geq A B$ ，直接写出点M横坐标m的取值范围．

查看试题解析
22. 如图， $Rt △ A B C$ 中， $∠ A C B = 90 °$ ，点D在 $B C$ 边上，以 $C D$ 为直径的 $⊙ O$ 与直线 $A B$ 相切于点E，且E是 $A B$ 中点，连接 $O A$ ．

(1)、求证： $O A = O B$ ；

(2)、连接 $A D$ ，若 $A D = \sqrt{7}$ ，求 $⊙ O$ 的半径．

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，点 $P (m ， y_{1})$ 在二次函数 $y = x^{2} + b x + c$ 的图象上，点 $Q (m ， y_{2})$ 在一次函数 $y = - x + 4$ 的图象上．

(1)、若二次函数图象经过点 $(0 ， 4)$ ， $(4 ， 4)$ ．
①求二次函数的解析式与图象的顶点坐标；

②判断 $m < 0$ 时， $y_{1}$ 与 $y_{2}$ 的大小关系；

(2)、若只有当 $m \geq 1$ 时，满足 $y_{1} \cdot y_{2} \leq 0$ ，求此时二次函数的解析式．

查看试题解析
24. 已知 $∠ M A N = 45 °$ ，点B为射线 $A N$ 上一定点，点C为射线 $A M$ 上一动点（不与点A重合），点D在线段 $B C$ 的延长线上，且 $C D = C B$ ．过点D作 $D E ⊥ A M$ 于点E．

(1)、当点C运动到如图 $1$ 的位置时，点E恰好与点C重合，此时 $A C$ 与 $D E$ 的数量关系是；

(2)、当点C运动到如图 $2$ 的位置时，依题意补全图形，并证明： $2 A C = A E + D E$ ；

(3)、在点C运动的过程中，点E能否在射线 $A M$ 的反向延长线上？若能，直接用等式表示线段 $A C$ ， $A E$ ， $D E$ 之间的数量关系；若不能，请说明理由．

查看试题解析
25. 如图 $1$ ，对于 $△ P M N$ 的顶点P及其对边 $M N$ 上的一点Q，给出如下定义：以P为圆心， $P Q$ 为半径的圆与直线 $M N$ 的公共点都在线段 $M N$ 上，则称点Q为 $△ P M N$ 关于点P的内联点．

在平面直角坐标系 $x O y$ 中：

(1)、如图 $2$ ，已知点 $A (7 ， 0)$ ，点 $B$ 在直线 $y = x + 1$ 上．
①若点 $B (3 ， 4)$ ，点 $C (3 ， 0)$ ，则在点O，C，A中，点是 $△ A O B$ 关于点B的内联点；

②若 $△ A O B$ 关于点B的内联点存在，求点B纵坐标n的取值范围；

(2)、已知点 $D (2 ， 0)$ ，点 $E (4 ， 2)$ ，将点D绕原点O旋转得到点F．若 $△ E O F$ 关于点E的内联点存在，直接写出点F横坐标m的取值范围．

查看试题解析

混入“HB”铅笔数	0	1	2
盒数	6	m	n