北京市东城区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-30 类型:期末考试
一、单选题
-
1. 使 有意义的x的取值范围是( )A、 B、 C、 D、2. 下列各式是最简二次根式的是( )A、 B、 C、 D、3. 若分式 的值为0,则x的值是( )A、 B、 C、 D、4. 下列各式中,运算正确的是( )A、 B、 C、 D、5. 2020年突如其来的新型冠状病毒肺炎疫情席卷全球,我国在党中央的坚强领导下,取得了抗击疫情的巨大成就.科学研究表明,某种新型冠状病毒颗粒的直径约为125纳米,1纳米 米,若用科学记数法表示125纳米,则正确的结果是( )A、 米 B、 米 C、 米 D、 米6. 下列各式由左到右是分解因式的是( )A、 B、 C、 D、7. 已知一个多边形的内角和为1080°,则这个多边形是( )A、九边形 B、八边形 C、七边形 D、六边形8. 如图所示,点O是 内一点, 平分 于点D , 连接 ,若 , ,则 的面积是( )
 A、20 B、30 C、50 D、1009. 如图, ,点P在边 上, ,点M、N在边 上, ,若 ,则 是( )
A、20 B、30 C、50 D、1009. 如图, ,点P在边 上, ,点M、N在边 上, ,若 ,则 是( )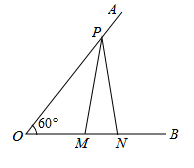 A、3 B、4 C、5 D、610. 剪纸是我国传统的民间艺术.如图①,②将一张纸片进行两次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A、3 B、4 C、5 D、610. 剪纸是我国传统的民间艺术.如图①,②将一张纸片进行两次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )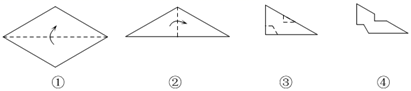 A、
A、 B、
B、 C、
C、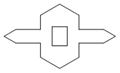 D、
D、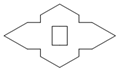
二、填空题
-
11. 因式分解: = .12. 如果 是一个完全平方式,那么m的值是 .13. 图(1)是一个长为2a , 宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是 .
 14. 如图所示,已知P是 上的一点, ,请再添加一个条件: , 使得 .
14. 如图所示,已知P是 上的一点, ,请再添加一个条件: , 使得 . 15. 小明同学用一根铁丝恰好围成一个等腰三角形,若其中两条边的长分别为 和 ,则这根铁丝的长为 .16. 如图,在 中,D是 上一点, ,则 °.
15. 小明同学用一根铁丝恰好围成一个等腰三角形,若其中两条边的长分别为 和 ,则这根铁丝的长为 .16. 如图,在 中,D是 上一点, ,则 °. 17. 如图,等腰直角 中, ,D为 的中点, ,若P为 上一个动点,则 的最小值为 .
17. 如图,等腰直角 中, ,D为 的中点, ,若P为 上一个动点,则 的最小值为 . 18. 如图, ,点 ,…在射线 上,点 ,…在射线 上,且 ,…均为等边三角形,以此类推,若 ,则 的边长为 .
18. 如图, ,点 ,…在射线 上,点 ,…在射线 上,且 ,…均为等边三角形,以此类推,若 ,则 的边长为 .
三、解答题
-
19. 计算: .20. 如图,点B,D,C,F在一条直线上, , , ,求证: .
 21. 已知 ,求代数式 的值.22. 尺规作图:
21. 已知 ,求代数式 的值.22. 尺规作图:如图所示,在一次军事演习中,红方侦察员发现:蓝方指挥部点P在A区内,且到铁路 和公路 的距离相等,到两通讯站C和D的距离也相等.如果你是红方的指挥员,请你在下图中标出蓝方指挥部点P的位置.(保留作图痕迹,不必写作法)
 23. 解方程: + =1.24. 先化简,再求值: ,其中 .25. 列分式方程解应用题:
23. 解方程: + =1.24. 先化简,再求值: ,其中 .25. 列分式方程解应用题:截止到2020年11月23日,全国832个国家级贫困县全部脱贫摘帽.某单位党支部在“精准扶贫”活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗.已知每棵乙种树苗的价格比甲种树苗的价格贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同,求甲、乙两种树苗每棵的价格.
26. 已知 是等边三角形,点D是 的中点,点P在射线 上,点Q在线段 上, . (1)、如图1,若点Q与点B重合,求证: ;(2)、如图2,若点P在线段 上, ,求 的值.27. 如图,在 中, ,D为 的中点,E为 延长线上一点,连接 ,过点D作 ,交 的延长线于点F , 连接 .作点B关于直线 的对称点G , 连接 .
(1)、如图1,若点Q与点B重合,求证: ;(2)、如图2,若点P在线段 上, ,求 的值.27. 如图,在 中, ,D为 的中点,E为 延长线上一点,连接 ,过点D作 ,交 的延长线于点F , 连接 .作点B关于直线 的对称点G , 连接 . (1)、依题意补全图形;(2)、若 .
(1)、依题意补全图形;(2)、若 .①求 的度数(用含 的式子表示);
②请判断以线段 为边的三角形的形状,并说明理由.
28. 如图,在平面直角坐标系 中,直线l经过点 ,且平行于y轴给出如下定义:点 先关于y轴对称得点 ,再将点 关于直线l对称得点 ,则称点 是点P关于y轴和直线l的二次反射点. (1)、已知 ,则它们关于y轴和直线l的二次反射点 , , 的坐标分别是;(2)、若点D的坐标是 ,其中 ,点D关于y轴和直线l的二次反射点是点 ,求线段 的长;(3)、已知点 ,点 ,以线段 为边在x轴上方作正方形 ,若点 , 关于y轴和直线l的二次反射点分别为 ,且线段 与正方形 的边有公共点,求a的取值范围.
(1)、已知 ,则它们关于y轴和直线l的二次反射点 , , 的坐标分别是;(2)、若点D的坐标是 ,其中 ,点D关于y轴和直线l的二次反射点是点 ,求线段 的长;(3)、已知点 ,点 ,以线段 为边在x轴上方作正方形 ,若点 , 关于y轴和直线l的二次反射点分别为 ,且线段 与正方形 的边有公共点,求a的取值范围.