北京市昌平区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 16的算术平方根是（）

A、2 B、±2 C、4 D、±4

查看试题解析
2. 如图， $△ A B C$ 中， $∠ B = 55 ° ， D$ 是 $B C$ 延长线上一点，且 $∠ A C D = 130 °$ ，则 $∠ A$ 的度数是（）

A、50 B、65 C、75 D、85

查看试题解析
3. （唐）元稹《长庆集》十五《景中秋》诗：“帘断萤火入，窗明蝙蝠飞.”蝙蝠省称“蝠”，因“蝠”与“福”谐音，人们以蝠表示福气，福禄寿喜等祥瑞，民间绘画中画五只蝙蝠，意为《五福临门》.下列图案一蝙蝠纹样是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如果一个三角形的三边长分别为5，8，a，那么a的值可能是（）

A、2 B、9 C、13 D、15

查看试题解析
5. 下列各式是最简二次根式的是（）

A、 $\sqrt{27}$ B、 $\sqrt{9}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{6}$

查看试题解析
6. 下列事件中，属于必然事件的是（）

A、小刚妈妈申请北京小客车购买指标，申请后第一次摇号时就中签 B、掷一枚骰子，向上一面的点数一定大于零 C、打开“学习强国APP”，正在播放歌曲《让爱暖人间》 D、用长度分别是 $3 cm ， 4 cm ， 8 cm$ 的细木条首尾顺次相连可组成一个三角形

查看试题解析
7. 根据下列表格信息，y可能为（）

x

$- 2$

$- 1$

0

1

2

y

0

无意义

A、 $\frac{x + 2}{x - 1}$ B、 $\frac{x - 2}{x + 1}$ C、 $\frac{x + 2}{x + 1}$ D、 $\frac{x - 2}{x - 1}$

查看试题解析
8. 如图， $△ A B C$ 是等边三角形，D是线段 $B C$ 上一点（不与点 $B ， C$ 重合），连接 $A D$ ，点 $E ， F$ 分别在线段 $A B ， A C$ 的延长线上，且 $D E = D F = A D$ ，点D从B运动到C的过程中， $△ B E D$ 周长的变化规律是（）

A、不变 B、一直变小 C、先变大后变小 D、先变小后变大

查看试题解析

二、填空题

9. 式子 $\sqrt{x - 3}$ 在实数范围内有意义，则 x 的取值范围是．

查看试题解析
10. 计算： $\frac{6}{a^{2} - 9} \div \frac{1}{a + 3} =$ ．

查看试题解析
11. 在 $△$ ABC中，AB=AC，点D在BC上（不与点B，C重合）．只需添加一个条件即可证明 $△$ ABD≌ $△$ ACD，这个条件可以是（写出一个即可）

查看试题解析
12. 请写出一个比 $\sqrt{10}$ 小的正整数．

查看试题解析
13. 口袋里有3个红球、2个白球、5个黄球，除颜色外都相同，从中随意摸出一个球，摸到白球的可能性的大小是．

查看试题解析
14. 如图，点C在 $∠ A O B$ 的平分线上， $C D ⊥ O A$ 于点D ，且 $C D = 2$ ，如果E是射线 $O B$ 上一点，那么 $C E$ 长度的最小值是．

查看试题解析
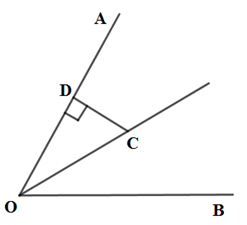15. 已知等腰三角形的一个内角为40°，则这个等腰三角形的顶角为．

查看试题解析
16. 如图， $△ A B C$ 中， $A B = B C$ ，点D在线段 $B C$ 上（不与点 $B ， C$ 重合）．

作法如下：

①连接 $A D$ ，作 $A D$ 的垂直平分线分别交直线 $A B ， A C$ 于点 $P ， Q$ ，连接 $D P ， D Q$ ，则 $△ A P Q ≌ △ D P Q$ ；

②过点D作 $A C$ 的平行线交 $A B$ 于点P ，在线段 $A C$ 上截取 $A Q$ ，使 $A Q = D P$ ，连接 $P Q ， D Q$ ，则 $△ A P Q ≌ △ D Q P$ ；

③过点D作 $A C$ 的平行线交 $A B$ 于点P ，过点D作 $A B$ 的平行线交 $A C$ 于点Q ，连接 $P Q$ ，则 $△ A P Q ≌ △ D Q P$ ；

④过点D作 $A B$ 的平行线交 $A C$ 于点Q ，在直线 $A B$ 上取一点P ，连接 $D P$ ，使 $D P = A Q$ ，连接 $P Q$ ，则 $△ A P Q ≌ △ D P Q$ ．以上说法一定成立的是．（填写正确的序号）

查看试题解析

三、解答题

17. 计算： $\sqrt{8} - \sqrt{3} \times \sqrt{6} + \sqrt{\frac{1}{2}} + | 1 - \sqrt{2} |$ ．

查看试题解析
18. 计算： $\frac{1}{x - y} - \frac{2 y}{x^{2} - y^{2}}$ ．

查看试题解析
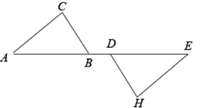
19. 解方程： $\frac{2 x}{x - 2} + \frac{3}{2 - x} = 1$ ．

查看试题解析
20. 已知：如图，点B，D在线段AE上，AD=BE，AC∥EH，∠C=∠H.求证：BC=DH.

查看试题解析
21. 已知： $x^{2} + x - 4 = 0$ ，求代数式 $(\frac{x}{x - 1} - 1) \div \frac{x^{3} - x}{x^{2} - 2 x + 1}$ 的值．

查看试题解析
22. 在正方形网格中，网格线的交点叫做格点，三个顶点均在格点上的三角形叫做格点三角形．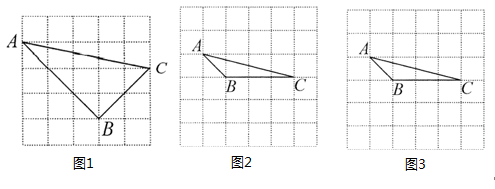

(1)、在图1中计算格点三角形 $A B C$ 的面积是；（每个小正方形的边长为1）

(2)、 $△ A B C$ 是格点三角形．
①在图2中画出一个与 $△ A B C$ 全等且有一条公共边 $B C$ 的格点三角形；

②在图3中画出一个与 $△ A B C$ 全等且有一个公共点A的格点三角形．

查看试题解析
23. 已知：如图， $∠ M O N$ 为锐角，点A在射线 $O M$ 上．

求作：射线 $A C$ ，使得 $A C // O N$ ．

小静的作图思路如下：

①以点A为圆心， $A O$ 为半径作弧，交射线 $O N$ 于点B ，连接 $A B$ ；

②作 $∠ M A B$ 的角平分线 $A C$ ．

射线 $A C$ 即为所求的射线．

(1)、使用直尺和圆规，按照小静的作图思路补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明： $∵ O A = A B$ ，

$∴ ∠ O = ∠ A B O$ （）．

$∵ ∠ M A B$ 是 $△ A O B$ 的一个外角，

$∴ ∠ M A B = ∠$ $+ ∠$ ．

$∴ ∠ A B O = \frac{1}{2} ∠ M A B$ ．

$∵ A C$ 平分 $∠ M A B$ ，

$∴ ∠ B A C = \frac{1}{2} ∠ M A B$ ．

$∴ ∠ A B O = ∠ B A C$ ．

$∴ A C // O N$ （）．

查看试题解析
24. 列方程解应用题
为了提高学生的身体素质，落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神，某校开展了“阳光体育天天跑活动”，初中男生、女生分别进行1000米和800米的计时跑步．在一次计时跑步中，某班一名女生和一名男生的平均速度相同，且这名女生跑完800米所用时间比这名男生跑完1000米所用时间少56秒，求这名女生跑完800米所用时间是多少秒．

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = A C = 2 ， ∠ B A C = 120^{°} ， A D ⊥ B C$ 于点D ，延长 $A D$ 至点E ，使 $D E = A D$ ，连接 $B E$ 和 $C E$ ．

(1)、补全图形；

(2)、若点F是 $A C$ 的中点，请在 $B C$ 上找一点P使 $A P + F P$ 的值最小，并求出最小值．

查看试题解析

26. 阅读理解

材料1：小学时常常会遇到将一个假分数写成带分数的问题，在这个计算的过程中，先计算分子中有几个分母求出整数部分，再把剩余的部分写成一个真分数，例如： $\frac{5}{3} = 1 + \frac{2}{3} = 1 \frac{2}{3}$ ．

类似的，我们可以将下列的分式写成一个整数与一个新分式的和．

例如： $\frac{x + 1}{x} = 1 + \frac{1}{x}$ ．

$\frac{x + 1}{x - 1} = \frac{(x - 1) + 2}{x - 1} = 1 + \frac{2}{x - 1}$ ．

材料2：为了研究字母x和分式 $\frac{1}{x}$ 值的变化关系，小明制作了表格，并得到数据如下：

x		$- 4$	$- 3$	$- 2$	$- 1$	0	1	2	3	4
$\frac{1}{x}$		$- 0.25$	$- 0. \dot{3}$	$- 0.5$	$- 1$	无意义	1	0.5	$0. \dot{3}$	0.25

请根据上述材料完成下列问题：

(1)、把下面的分式写成一个整数与一个新分式的和的形式：

$\frac{x + 2}{x} =$ ； $\frac{x + 1}{x - 2} =$ ；

(2)、当

x > 0

时，随着x的增大，分式

\frac{x + 2}{x}

的值（增大或减小）；

(3)、当

x > - 1

时，随着x的增大，分式

\frac{2 x + 3}{x + 1}

的值无限趋近一个数，请写出这个数，并说明理由．

查看试题解析

27. 在 $△ A B C$ 中， $A B = A C ， ∠ B A C = 90^{°}$ ．

(1)、如图1，点 $P ， Q$ 在线段 $B C$ 上， $A P = A Q ， ∠ B A P = 15^{°}$ ，求 $∠ A Q B$ 的度数；

(2)、点 $P ， Q$ 在线段 $B C$ 上（不与点 $B ， C$ 重合）， $A P = A Q$ ，点Q关于直线 $A C$ 的对称点为M ，连接 $A M ， P M$ ．
①依题意将图2补全；

②用等式表示线段 $B P ， A P ， P C$ 之间的数量关系，并证明．

查看试题解析
28. 定义：点P是 $△ A B C$ 内部的一点，若经过点P和 $△ A B C$ 中的一个顶点的直线把 $△ A B C$ 平分成两个面积相等的图形，则称点P是 $△ A B C$ 关于这个顶点的均分点．例如图中，点P是 $△ A B C$ 关于顶点A的均分点．

(1)、下列图形中，点D一定是 $△ A B C$ 关于顶点B的均分点的是；（填序号）

(2)、在 $△ A B C$ 中， $B C = 2 ， A B = A C$ 且 $A B > B C$ ，点P是 $△ A B C$ 关于顶点A的均分点，且 $\sqrt{2} ⩽ B P ⩽ 2$ ，直接写出 $∠ B P C$ 的范围；

(3)、如图，在 $△ A B C$ 中， $∠ B A C = 90^{°} ， B C = 10$ ，点P是 $△ A B C$ 关于顶点A的均分点，直线 $A P$ 与 $B C$ 交于点D ，当 $B P ⊥ A D$ 时， $B P = 4$ ，求 $C P$ 的长．

查看试题解析