安徽省芜湖市2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-09-30 类型:期末考试
一、单选题
-
1. -2021的倒数是( )A、2021 B、 C、-2021 D、2. 山东省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示( )A、5.47×108 B、0.547×108 C、547×105 D、5.47×1073. 下列说法正确的是( )A、 的系数是-5 B、单项式x的系数为1,次数为0 C、 是二次三项式 D、 的次数是64. 一个正方体的每个面上各写一个汉字,它的表面展开图如图所示,那么正方体中与“古”字相对的面的汉字是( )
 A、芜 B、湖 C、鸠 D、兹5. 下列运算正确的是( )A、 B、 C、 D、6. 长方形按如图所示折叠,点 折叠到点 的位置,已知 ,则 等于( )
A、芜 B、湖 C、鸠 D、兹5. 下列运算正确的是( )A、 B、 C、 D、6. 长方形按如图所示折叠,点 折叠到点 的位置,已知 ,则 等于( ) A、56° B、58° C、59° D、60°7. 若关于 的方程 的解是-7,则 的值为( )A、-4 B、4 C、2 D、-28. 在时刻8:30,时钟上的时针和分针之间的夹角为( )A、85° B、75° C、70° D、60°9. 一只猎犬发现前方100米处有一头野猪以10米/秒的速度向正前方逃窜,猎犬立即以15米/秒的速度追赶(猎犬追赶路线与野猪逃跑路线在一条直线上),猎犬多少秒后可以追上野猪?若设猎犬 秒可追上野猪,根据题意,可列方程为( )A、 B、 C、 D、10.
A、56° B、58° C、59° D、60°7. 若关于 的方程 的解是-7,则 的值为( )A、-4 B、4 C、2 D、-28. 在时刻8:30,时钟上的时针和分针之间的夹角为( )A、85° B、75° C、70° D、60°9. 一只猎犬发现前方100米处有一头野猪以10米/秒的速度向正前方逃窜,猎犬立即以15米/秒的速度追赶(猎犬追赶路线与野猪逃跑路线在一条直线上),猎犬多少秒后可以追上野猪?若设猎犬 秒可追上野猪,根据题意,可列方程为( )A、 B、 C、 D、10.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是( )
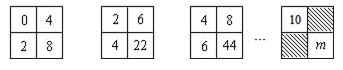 A、110 B、158 C、168 D、17811. 设“●■▲”分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么“?”处应该放“●”的个数为( )
A、110 B、158 C、168 D、17811. 设“●■▲”分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么“?”处应该放“●”的个数为( ) A、4 B、3 C、2 D、112. 对于两个不相等的有理数 , ,我们规定符号 表示 , 两数中较大的数,例如 .则方程 的解为( )A、-1 B、-2 C、-1或-2 D、1或2
A、4 B、3 C、2 D、112. 对于两个不相等的有理数 , ,我们规定符号 表示 , 两数中较大的数,例如 .则方程 的解为( )A、-1 B、-2 C、-1或-2 D、1或2二、填空题
-
13. 若 、 互为相反数,则 的值为 .14. 一个角是它的补角的五分之一,则这个角的余角是度.15. 已知 ,则 .16. 某种商品第一次降价每件减10元,第二次降价是在第一次降价的基础上打“八折”出售的,两次降价后每件的价格是m元,则该商品的原价每件是元.17. 甲、乙两站相距 ,一列慢车从甲站开往乙站,每小时行 ,一列快车从乙站开往甲站,每小时行 .已知慢车先行 ,快车再开出,则快车开出 与慢车相遇.18. 如图,数轴上点 , , 对应的有理数分别是 , , , ,且 ,则 .

三、解答题
-
19. 先化简,再求值: ,其中x= .20. 如图,同一行的两个图形中小正方形的个数相等,但它们的排列方式不一样,根据不同的排列方式可以得到一列等式.

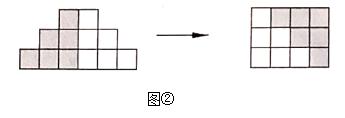
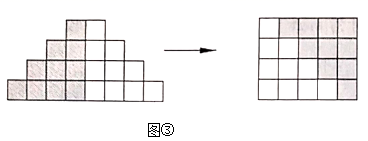 (1)、第 个图形中对应的等量关系是 .(2)、根据(1)的结论,求 的值.21. 如图, , 是线段 的三等分点, 是线段 上一点, 比 长 ,求 的长.
(1)、第 个图形中对应的等量关系是 .(2)、根据(1)的结论,求 的值.21. 如图, , 是线段 的三等分点, 是线段 上一点, 比 长 ,求 的长. 22. 一家服装店在换季时积压了一批服装.为了缓解资金的压力,决定打折销售.其中一条裤子的成本为80元,按标价五折出售将亏30元,(1)、求这条裤子的标价是多少元?(2)、另一件上衣按标价打九折出售,和这条裤子合计卖了230元,两件衣服恰好不赢不亏,求这件上衣的标价是多少元?23. 如图,直角三角板的直角边 在直线 上,作射线 ,使 .
22. 一家服装店在换季时积压了一批服装.为了缓解资金的压力,决定打折销售.其中一条裤子的成本为80元,按标价五折出售将亏30元,(1)、求这条裤子的标价是多少元?(2)、另一件上衣按标价打九折出售,和这条裤子合计卖了230元,两件衣服恰好不赢不亏,求这件上衣的标价是多少元?23. 如图,直角三角板的直角边 在直线 上,作射线 ,使 . (1)、三角板绕直角顶点 逆时针旋转,当直角边 在 的内部,直角边 在直线 的下方时:
(1)、三角板绕直角顶点 逆时针旋转,当直角边 在 的内部,直角边 在直线 的下方时:①若 ,求 的度数;
②若 ,求 的度数(用含 的代数式表示);
(2)、若三角板绕点 按每秒7°的速度逆时针旋转一周,在旋转的过程中,经过多少秒时,射线 恰好是 的平分线?