安徽省桐城市2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 在0，-3，2，-2四个数中，最小的数是（）

A、0 B、-3 C、2 D、-2

查看试题解析
2. 据统计，某城市去年接待旅游人数约为89000000人，89000000这个数据用科学记数法表示为（）

A、 $8.9 \times 10^{5}$ B、 $8.9 \times 10^{6}$ C、 $8.9 \times 10^{7}$ D、 $8.9 \times 10^{8}$

查看试题解析
3. 今年某校有2000名学生参加线上学习，为了解这些学生的数学成绩，从中抽取100名考生的数学成绩进行统计分析，以下说法正确的是（）

A、2000名学生是总体 B、每名学生的数学成绩是个体 C、100名学生是样本 D、100名学生是样本容量

查看试题解析
4. 一个长方形的长是 $2 a$ ，宽是 $a + 1$ ，则这个长方形的周长为（）

A、 $6 a + 1$ B、 $2 a^{2} + 2 a$ C、 $3 a + 1$ D、 $6 a + 2$

查看试题解析
5. 下列说法正确的是（）

A、两点之间的所有连线中，直线最短 B、一个角的余角一定比这个角大 C、同角（或等角）的补角相等 D、经过两点有无数条直线

查看试题解析
6. 有理数 $a$ ， $b$ 的对应点在数轴上的位置如图所示，下列结论正确的是（）

A、 $a + b > 0$ B、 $a b > 0$ C、 $a - b > 0$ D、 $- a + b > 0$

查看试题解析
7. 定义运算 $a ★ b = | a b - 2 a - b |$ ，如 $1 ★ 3 = | 1 \times 3 - 2 \times 1 - 3 | = 2$ ，则 $- 2 ★ 4$ 的值为（）

A、8 B、-8 C、16 D、-16

查看试题解析
8. 某商品每件标价为150元，若按标价打8折后，再降价10元销售，仍获利10元，则该商品每件的进价为（）

A、100元 B、105元 C、110元 D、120元

查看试题解析
9. 如图，已知 $∠ A O B = 90^{°}$ ， $O C$ 是 $∠ A O B$ 内任意一条射线， $O B ， O D$ 分别平分 $∠ C O D$ ， $∠ B O E$ ，下列结论：① $∠ C O D = ∠ B O E$ ；② $∠ C O E = 3 ∠ B O D$ ；③ $∠ B O E = ∠ A O C$ ；④ $∠ A O C + ∠ B O D = 90^{°}$ ，其中正确的有（）

A、①②④ B、①③④ C、①②③ D、②③④

查看试题解析
10. 如图，在大长方形ABCD中，放入六个相同的小长方形，则阴影部分的面积为（）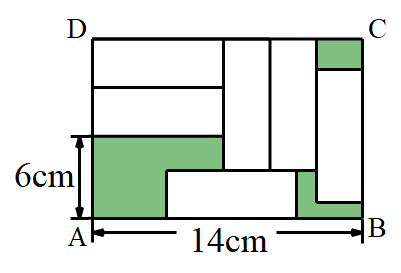

A、140 cm2 B、96cm2 C、44 cm2 D、16 cm2

查看试题解析

二、填空题

11. 若单项式 $- x y^{a + 1}$ 与 $2 x^{b - 2} y^{3}$ 的和仍是一个单项式，则 $a^{b} =$ ．

查看试题解析
12. 如图，已知线段 $A B = 8 cm$ ， $M$ 是 $A B$ 的中点，P是线段 $M B$ 上一点，N为 $P B$ 的中点， $N B = 1.5 cm$ ，则线段 $M P =$ $cm$ ．

查看试题解析
13. 把所有正偶数从小到大排列，并按如下规律分组：（2）， $(4 ， 6)$ ， $(8 ， 10 ， 12)$ ， $(14 ， 16 ， 18 ， 20)$ …，现有等式 $A {m} = (i ， j)$ 表示正偶数 $m$ 是第 $i$ 组第 $j$ 个数（从左往右数），如 $A {2} = (1 ， 1)$ ， $A {10} = (3 ， 2)$ ， $A {18} = (4 ， 3)$ ，则 $A {40} =$ ．

查看试题解析
14. 在如图所示的运算程序中，若开始输入的 $x$ 值为24，我们发现第1次输出的结果为12，第2次输出的结果为6，……，则第2021次输出的结果为．

查看试题解析

三、解答题

15. 计算： $- 3^{2} - \frac{1}{3} \times [{(- 5)}^{2} \times (- \frac{3}{5}) + 60 \div (- 4)]$ ．

查看试题解析
16. 解方程： $\frac{x - 1}{2} - \frac{4 x - 2}{3} = 1$ ．

查看试题解析
17. 先化简，再求值：
已知a、b满足 $| a - \frac{1}{2} | + {(b + \frac{2}{3})}^{2} = 0$ ，求代数式 $4 a b - [3 a b - 2 (4 a b^{2} + \frac{1}{2} a b)] - 5 a b^{2}$ 的值

查看试题解析
18. 如图，在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛，若圆形的半径为 $r$ 米，广场长为 $a$ 米，宽为 $b$ 米．

(1)、请列式表示广场空地的面积（结果保留 $π$ ）；

(2)、若休闲广场的长为300米，宽为100米，圆形花坛的半径为20米，求广场空地的面积（ $π$ 取3.14）．

查看试题解析
19. 某人今日从A地乘一辆汽车沿东西方向行驶，约定向东走为正，下车后观察行走记录（单位：km）：+5， $-$ 2，+4， $-$ 1，+10， $-$ 3， $-$ 2， $-$ 10，求：

(1)、下车时，此人在A地的哪一边，距A地多远？

(2)、若汽车耗油2升/每千米，此人今日用了多少升汽油？

查看试题解析
20. 某校开展校园艺术节系列活动，校学生会代表小亮到文体超市购买文具作为奖品．

(1)、小亮第一次购买若干个文具袋作为奖品，这种文具袋标价每个10元，请认真阅读结账时老板与小亮的对话图片，求小亮原计划购买文具袋多少个？

(2)、小亮第二次购买钢笔和签字笔共50支作为补充奖品，其中钢笔标价每支8元，签字笔标价每支6元．经过沟通，这次老板给予8折优惠，钢笔和签字笔合计288元，问小亮购买了钢笔和签字笔各多少支？

查看试题解析
21. 新学期，某校开设了“防疫宣传”“心理疏导”等课程，为了解学生对新开设课程的掌握情况，从八年级学生中随机抽取了部分学生进行了一次综合测试．测试结果分为四个等级： $A$ 级为优秀， $B$ 级为良好， $C$ 级为及格， $D$ 级为不及格．将测试结果绘制了两幅不完整的统计图．根据统计图中的信息解答下列问题：

(1)、本次抽样测试的学生人数是名；

(2)、扇形统计图中表示 $A$ 级的扇形圆心角 $α$ 的度数是 ▲ ，并把条形统计图补充完整；

(3)、该校八年级共有学生400名，如果全部参加这次测试，估计优秀的人数为多少？

查看试题解析
22. “分类讨论”是一种重要数学思想方法，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的四个问题．
例：三个有理数 $a$ ， $b$ ， $c$ 满足 $a b c > 0$ ，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值．

解：由题意得， $a$ ， $b$ ， $c$ 三个有理数都为正数或其中一个为正数，另两个为负数．

①当 $a$ ， $b$ ， $c$ 都是正数，即 $a > 0$ ， $b > 0$ ， $c > 0$ 时，

则： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = \frac{a}{a} + \frac{b}{b} + \frac{c}{c} = 1 + 1 + 1 = 3$ ，

②当 $a$ ， $b$ ， $c$ 有一个为正数，另两个为负数时，设 $a > 0$ ， $b < 0$ ， $c < 0$ ，

则： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = \frac{a}{a} + \frac{- b}{b} + \frac{- c}{c} = 1 + (- 1) + (- 1) = - 1$ ．

综上， $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为3或-1．

请根据上面的解题思路解答下面的问题：

(1)、已知 $| a | = 3$ ， $| b | = 1$ ，且 $a < b$ ，求a+b的值；

(2)、已知 $a$ ， $b$ 是有理数，当 $a b > 0$ 时，求 $\frac{a}{| a |} + \frac{b}{| b |}$ 的值．

(3)、已知 $a$ ， $b$ ， $c$ 是有理数， $a + b + c = 0$ ， $a b c < 0$ ，求 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |}$ ．

查看试题解析
23. 如图1，将一副三角板的直角顶点 $C$ 叠放在一起．

(1)、（观察分析）
若 $∠ D C E = 35 °$ ，则 $∠ A C B =$ ；若 $∠ A C B = 150 °$ ，则 $∠ D C E =$ ．

(2)、（猜想探究）
请你猜想 $∠ A C B$ 与 $∠ D C E$ 有何关系，并说明理由；

(3)、（拓展应用）
如图2，若将两个同样的三角尺 $60 °$ 锐角的顶点 $A$ 重合在一起，请你猜想 $∠ D A B$ 与 $∠ C A E$ 有何关系，并说明理由．

查看试题解析