安徽省淮北市2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-09-30 类型:期末考试
一、单选题
-
1. 下列各数: , , , , 中,有理数有( )A、1个 B、2个 C、3个 D、4个2. 当 时, 等于( )A、0 B、1 C、2 D、33. 餐桌边的一蔬一饭,舌尖上的一饮一酌,实属来之不易,舌尖上的浪费让人触目惊心.据统计,中国每年浪费的食物总量折合粮食约500亿千克,这个数据用科学记数法表示为( )千克.A、 B、 C、 D、4. 若单项式 与 是同类项,则 的值为( )A、9 B、8 C、6 D、55. 若 , , ,则有( )A、 B、 C、 D、6. 已知点 、 、 都是直线 上的点,且 , ,那么点 与点 之间的距离是( )A、 B、 或 C、 D、 或7. 若方程组 的解是 则方程组 的解是( )A、 B、 C、 D、8. 如图,点 、 、 在同一条直线上,则下列说法正确的是( )
 A、射线 和射线 是同一条射线 B、直线 和直线 是同一条直线 C、图中只有 条线段 D、图中有 条直线9. 下面是反映世界人口情况的数据:1957年、1974年、1987年、1999年的世界人口数依次为30亿、40亿、50亿、60亿,2011年世界人口将达70亿,预计2050年世界人口将达90亿.上面的数据不能制成( )A、统计表 B、条形统计 C、折线统计 D、扇形统计图10. 如图,直线 外有一定点 ,点 是直线 上的一个动点,当点 从右向左运动时, 和 的关系是( )
A、射线 和射线 是同一条射线 B、直线 和直线 是同一条直线 C、图中只有 条线段 D、图中有 条直线9. 下面是反映世界人口情况的数据:1957年、1974年、1987年、1999年的世界人口数依次为30亿、40亿、50亿、60亿,2011年世界人口将达70亿,预计2050年世界人口将达90亿.上面的数据不能制成( )A、统计表 B、条形统计 C、折线统计 D、扇形统计图10. 如图,直线 外有一定点 ,点 是直线 上的一个动点,当点 从右向左运动时, 和 的关系是( )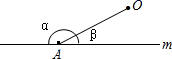 A、 越来越小 B、 越来越大 C、 D、 和 均保持不变
A、 越来越小 B、 越来越大 C、 D、 和 均保持不变二、填空题
-
11. 的相反数是 , 倒数是 .12. 在修建高速公路遇到大山的阻挡时,为了尽量缩短公路里程,往往需要开凿隧道,其所遵循的数学原理是 .13. 如图,一副三角板(直角顶点重合)摆放在桌面上,若 ,则 .
 14. 在扇形统计图中,其中一个扇形的圆心角是 ,则这个扇形所表示的部分占总体的百分数是 .15. 希腊数学家将数:1,3,6,10,15,21,28,…,叫做三角形数,它有一定的规律性,第17个三角形数与第15个三角形数的差为 .
14. 在扇形统计图中,其中一个扇形的圆心角是 ,则这个扇形所表示的部分占总体的百分数是 .15. 希腊数学家将数:1,3,6,10,15,21,28,…,叫做三角形数,它有一定的规律性,第17个三角形数与第15个三角形数的差为 .三、解答题
-
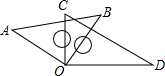
16. 计算 .17. 解方程(组)(1)、解方程: ;(2)、解方程组: .18. 先化简,再求值: ,其中 , .19. 我国民间流传着许多趣味算题,它们多以顺口溜的形式表达,其中《孙子算经》中记载了这样一个数学问题:一群老头去赶集,半路买了一堆梨,一人一个多一梨,一人两个少二梨,请问君子知道否,几个老头几个梨?20. 如图, 为直角, 为锐角,且 平分 , 平分 ,
 (1)、如果 ,求 的度数.(2)、如果 为任意一个锐角,你能求出 的度数吗?若能,请求出来,若不能,说明为什么?21. 图①、图②反映是东方百货商场今年1-5月份的商品销售额统计情况观察图①和图②,解答下面问题:
(1)、如果 ,求 的度数.(2)、如果 为任意一个锐角,你能求出 的度数吗?若能,请求出来,若不能,说明为什么?21. 图①、图②反映是东方百货商场今年1-5月份的商品销售额统计情况观察图①和图②,解答下面问题: (1)、来自商场财务部的报告表明,商场1-5月份的销售总额一共是370万元,请你根据这一信息补全图①,并写出两条由上两图获得的信息;(2)、商场服装部5月份的销售额是多少万元?(3)、李强观察图②后认为,5月份服装部的销售额比4月份减少了你同意他的看法吗?为什么?22. 已知:如图1,点O是直线AB上的一点.
(1)、来自商场财务部的报告表明,商场1-5月份的销售总额一共是370万元,请你根据这一信息补全图①,并写出两条由上两图获得的信息;(2)、商场服装部5月份的销售额是多少万元?(3)、李强观察图②后认为,5月份服装部的销售额比4月份减少了你同意他的看法吗?为什么?22. 已知:如图1,点O是直线AB上的一点. (1)、如图1,当∠AOD是直角时,3∠AOC=∠BOD , 求∠COD的度数;(2)、若∠COD保持在(1)中的大小不变,它绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD , 则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;(3)、若∠COD从(1)中的位置开始,边OC、边OD分别绕着点O以每秒20°、每秒10°的速度顺时针旋转(当其中一边与OB重合时都停止旋转),OM、ON分别平分∠BOC、∠BOD .
(1)、如图1,当∠AOD是直角时,3∠AOC=∠BOD , 求∠COD的度数;(2)、若∠COD保持在(1)中的大小不变,它绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD , 则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;(3)、若∠COD从(1)中的位置开始,边OC、边OD分别绕着点O以每秒20°、每秒10°的速度顺时针旋转(当其中一边与OB重合时都停止旋转),OM、ON分别平分∠BOC、∠BOD .求:①运动多少秒后,∠COD=10°;
②运动多少秒后,∠COM=∠BON .