安徽省合肥市包河区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 在数0， $- | - 2 |$ ，-0.5， $- (- \frac{2}{3})$ 中，负数的个数是（）

A、3 B、2 C、1 D、0

查看试题解析
2. 2020年9月11日，巢湖水位终于回落至警戒水位10.50米，这意味着“巢湖保卫战”取得重大胜利．在这场浩大的洪水之战中，合肥市前后出动了超过155万人次抗洪，而数字155万用科学记数法表示为（）

A、 $1.55 \times 10^{6}$ B、 $1.55 \times 10^{5}$ C、 $1.55 \times 10^{2}$ D、 $1.55 \times 10^{4}$

查看试题解析
3. 关于 $x$ 的一元一次方程 $2 x - 2 + m = 4$ 的解为 $x = 1$ ，则 $m$ 的值为（）

A、6 B、5 C、4 D、3

查看试题解析
4. 若 $\frac{2 x - 1}{3} = 5$ 与 $k x - 1 = 15$ 的解相同，则 $k$ 的值为（）

A、8 B、6 C、－2 D、2

查看试题解析
5. 某校对学校上学方式进行了一次抽样调查，如图是根据此次调查结果所绘制的扇形统计图，已知该学校共2560人，被调查的学生中骑车的有21人，则下列四中说法中，错误的是（）

A、被调查的学生有60人 B、被调查的学生中，步行的有27人 C、估计全校骑车上学的学生有1152人 D、扇形图中，乘车部分所对应的圆心角为54°

查看试题解析
6. 已知线段 $A B = 10 c m$ ，线段 $A C = 16 c m$ ，且 $A B$ 、 $A C$ 在同一条直线上，点 $B$ 在 $A$ 、 $C$ 之间，此时 $A B$ 、 $A C$ 的中点 $M$ 、 $N$ 之间的距离为（）

A、13cm B、6cm C、3cm D、1.5cm

查看试题解析
7. 如图，直线AB，CD相交于点O，OE⊥AB于O，∠COE=55°，则∠BOD的度数是（）

A、35° B、45° C、30° D、40°

查看试题解析
8. 若四条直线在平面内交点的个数为 $a$ ，则 $a$ 的可能取值有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
9. 某超市在“元旦”活动期间，推出如下购物优惠方案：
①一次性购物在100元（不含100元）以内，不享受优惠；②一次性购物在100元（含100元）以上，350元（不含350元）以内，一律享受九折优惠；③一次性购物在350元（含350元）以上，一律享受八折优惠；小敏在该超市两次购物分别付了85元和270元，如果小敏把这两次购物改为一次性购物，则小敏至少需付款（）元

A、284 B、308 C、312 D、320

查看试题解析
10. 用如图①中的长方形和正方形纸板作侧面和底面，做成如图②的竖式和横式的两种无盖纸盒。现在仓库里有若干张正方形和若干张长方形纸板，如果做两种纸盒若干个，恰好使库存的纸板用完，则库存中正方形纸板与长方形纸板之和的值可能是（）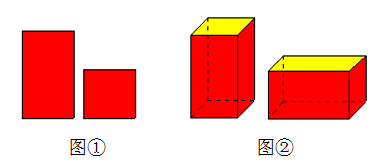

A、2018 B、2019 C、2020 D、2021

查看试题解析

二、填空题

11. ﹣0.5的相反数是，倒数是.

查看试题解析
12. 若代数式 $x - 2 y = - 3$ ，则代数式 $4 y - 2 x + 1$ 的值为．

查看试题解析
13. 已知： $A$ 和 $B$ 都在同一条数轴上，点 $A$ 表示 $- 2$ ，又知点 $B$ 和点 $A$ 相距 $5$ 个单位长度，则点 $B$ 表示的数一定是．

查看试题解析
14. 按如图所示的运算程序进行运算：则当输入的数为时，运算后输出结果为8．

查看试题解析
15. 某同学晚上6点多钟开始做作业，他家墙上时钟的时针和分针的夹角是120°，他做完作业后还是6点多钟，且时针与分针的夹角还是120°，此同学做作业用了分针．

查看试题解析
16. 如图， $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ， $∠ A O C = 30 °$ ，将一直角三角板（ $∠ M = 30 °$ ）的直角顶点放在点 $O$ 处，一边 $O N$ 在射线 $O A$ 上，另一边 $O M$ 与 $O C$ 都在直线 $A B$ 的上方．将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．经过秒后， $O M$ 恰好评分 $∠ B O C$ ；若三角板在转动的同时，射线 $O C$ 也绕 $O$ 点以每秒5°的速度沿顺时针方向旋转一周，如图，那么经过秒， $O C$ 平分 $∠ M O N$ ？

查看试题解析

三、解答题

17.

(1)、计算： $- 2^{3} \times (1 - \frac{1}{4}) \div 0.5$

(2)、解方程： $\frac{2 x + 1}{4} - 1 = \frac{x}{6} - \frac{5 x - 1}{3}$

查看试题解析
18. 先化简，再求值：（2x²-5x+4）-3（x²-x+1），期中x＝-2.

查看试题解析
19. 某学校组织七年级学生参加了“热爱宪法，捍卫宪法”的知识竞赛，从中抽取了部分学生成绩（得分取正整数，满分为100分）进行统计，绘制统计图如下．请根据所给信息，回答下列问题：
某校七年级部分学生成绩频数分布直方图

某校七年级部分学生成绩扇形统计图

(1)、求出 $A$ 组、 $B$ 组人数分别占总人数的百分比；

(2)、求本次共抽查了多少名学生的成绩；

(3)、扇形统计图中， $D$ 组对应的圆心角为 $a °$ ，求 $a$ 的值；

(4)、该区共有1000名七年级学生参加了此次竞赛，若主办方想把一等奖的人数控制在150人，那么请你通过计算估计：一等奖的分值应定在多少分及以上？

查看试题解析
20. 如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着-5，-2，1，9，且任意相邻四个台阶上数的和都相等．

(1)、求第5个台阶上的数 $x$ 是多少？

(2)、试用含 $k$ （ $k$ 为正整数）的式子表示出数“1”所在的台阶数（此问直接写出结果）．

查看试题解析
21. 某水果店有甲，乙两种水果，它们的单价分别为 $a$ 元/千克， $b$ 元/千克．若购买甲种水果5千克，乙种水果2千克，共花费25元，购买甲种水果3千克，乙种水果4千克，共花费29元.

(1)、求 $a$ 和 $b$ 的值；

(2)、甲种水果涨价 $m$ 元/千克 $(0 < m < 2)$ ，乙种水果单价不变，小明花了45元购买了两种水果10千克，那么购买甲种水果多少千克？（用含 $m$ 的代数式表示）．

查看试题解析
22. 点 $A$ 在数轴上对应的数为 $a$ ，点 $B$ 对应的数为 $b$ ，且 $a$ 、 $b$ 满足 $| a + 5 | + {(b - 3)}^{2} = 0$ ．

(1)、求点 $A$ ， $B$ 所表示的数；

(2)、点 $P$ 在直线 $A B$ 上点 $B$ 右边一点，且 $A P = b P B$ ，点 $Q$ 为 $P B$ 的中点，求线段 $A Q$ 的长．

查看试题解析
23. 已知点 $O$ 为直线 $A B$ 上一点，将直角三角板 $M O N$ 如图所示放置，且直角顶点在 $O$ 处，在 $∠ M O N$ 内部作射线 $O C$ ，且 $O C$ 恰好评分 $∠ M O B$ ．

(1)、若 $∠ C O N = 10 °$ ，求 $∠ A O M$ 的度数；

(2)、若 $∠ B O N = 2 ∠ N O C$ ，求 $∠ A O M$ 的度数；

(3)、试猜想 $∠ A O M$ 与 $∠ N O C$ 之间的数量关系，并说明理由．

查看试题解析