安徽省滁州市全椒县2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 2021的倒数是（）

A、 $\frac{1}{2021}$ B、﹣ $\frac{1}{2021}$ C、﹣2021 D、2021

查看试题解析
2. 自2019年末到2020年4月底世界各国感染新型冠状肺炎病毒患者约为331万人，将数据331万用科学记数法表示为（）

A、 $331 \times 10^{4}$ B、 $33.1 \times 10^{5}$ C、 $3.31 \times 10^{6}$ D、 $3.31 \times 10^{7}$

查看试题解析
3. 下列调查中，适合采用全面调查的是（）

A、对中学生目前睡眠质量的调查 B、开学初，对进入我校人员体温的测量 C、对我市中学生每天阅读时间的调查 D、对我市中学生在家学习网课情况的调查

查看试题解析
4. 单项式 $- 2 x y^{b + 1}$ 与 $\frac{1}{3} x^{a - 2} y^{3}$ 是同类项，则下列单项式与它们属于同类项的是（）

A、 $- 5 x^{3} y$ B、 $3 x y^{3}$ C、 $2 x^{3} y^{2}$ D、 $x y$

查看试题解析
5. 点A，B在数轴上的位置如图所示，其对应的数分别是a和b.对于以下结论：

甲：b−a<0；乙：a+b>0；丙：|a|<|b|；丁： $\frac{b}{a}$ >0；其中正确的是（）

A、甲乙 B、丙丁 C、甲丙 D、乙丁

查看试题解析
6. 如图，点O在直线 $E D$ 上， $∠ A O B = ∠ C O D 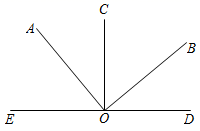= 90 °$ ，下列说法错误的是（）

A、 $∠ A O C = ∠ B O D$ B、 $∠ A O E$ 和 $∠ A O C$ 互余 C、 $∠ A O E = ∠ B O D$ D、 $∠ A O C$ 和 $∠ B O E$ 互补

查看试题解析
7. 把某一段公路的一侧全部栽上银杏树，要求路的两端各栽一棵，并且每两棵树的间隔相等．如果每隔 $5$ 米栽 $1$ 棵，则树苗缺 $21$ 棵；如果每隔 $6$ 米栽 $1$ 棵，则树苗正好用完．设原有树苗 $x$ 棵，公路长为 $y$ 米．根据题意，下面所列方程组中正确的是（）

A、 ${\begin{array}{l} y = 6 (x - 1) \\ 5 (x + 21 - 1) = y \end{array}$ B、 ${\begin{array}{l} y = 6 (x - 1) \\ 5 (x + 21) = y \end{array}$ C、 ${\begin{array}{l} y = 6 x \\ 5 (x + 21 - 1) = y \end{array}$ D、 ${\begin{array}{l} y = 6 x \\ 5 (x + 21) = y \end{array}$

查看试题解析
8. 已知线段 $A B ， C$ 是直线 $A B$ 上的一点 $, A B = 8, B C = 4$ ，点 $M$ 是线段 $A C$ 的中点，则线段 $A M$ 的长为（）

A、2 B、4 C、4或6 D、2或6

查看试题解析
9. 如图是小强用火柴棒搭的1条，2条，3条“金鱼”，…则搭n条“金鱼”需要火柴棒的根数是（）

A、7n+1 B、 $6 n + 2$ C、 $5 n + 3$ D、 $4 n + 4$

查看试题解析
10. 若关于x，y的方程组 ${\begin{array}{l} 2 x + 3 y = 4 \\ 3 x + 2 y = 2 m - 3 \end{array}$ 的解满足 $x + y = - \frac{3}{5}$ ，则m的值是（）

A、-2 B、-1 C、0 D、 $\frac{3}{2}$

查看试题解析

二、填空题

11. 已知 $a + b = 3$ ，则 $2 - a - b =$ ．

查看试题解析
12. 若关于x，y的代数式 $x^{3} - 2 a x y + a x^{3} + \frac{1}{2} x y - 5$ 不含二次项，则 $a =$ ．

查看试题解析
13. 如图，已知∠COB＝2∠AOC ， OD平分∠AOB ，且∠COD＝18°，则∠AOB的度数为．

查看试题解析
14. 一列数 $a_{1} ， a_{2} ， a_{3} ， \cdot \cdot \cdot ， a_{n}$ ，其中 $a_{1} = - 1 ， a_{2} = \frac{1}{1 - a_{1}} ， a_{3} = \frac{1}{1 - a_{2}} ， \cdot \cdot \cdot ， a_{n} = \frac{1}{1 - a_{n - 1}}$ ，则 $a_{2021} =$ ．

查看试题解析

三、解答题

15. 计算： $- 1^{4} + {(- 2)}^{3} \times (- \frac{1}{2}) - (- 3^{2})$ ．

查看试题解析
16. 解方程（组）

(1)、解方程： $1 + \frac{x}{2} = \frac{8 - 2 x}{3}$

(2)、解方程组 ${\begin{array}{l} x - 4 y = - 3 \\ x + 2 y = 3 \end{array}$

查看试题解析
17. 现规定一种运算法则※，对于任意两个有理数a，b，有 $a ※ b = 2 a - a b$ ，例如 $1 ※ 3 = 2 \times 1 - 1 \times 3 = - 1$ ．

(1)、计算 $- 2 ※ 5$ ；

(2)、若 $(x - 1) ※ 4 = \frac{1}{2} ※ x$ ，求x的值．

查看试题解析
18. 如图，点B，C把线段 $A D$ 分成2∶5∶3三部分，点M为 $A D$ 的中点， $B M = 12$ ，求 $C M$ 和 $A D$ 的长．

查看试题解析
19. 已知 $A = 3 a^{2} b - 2 a b^{2} + a b c$ ，小明错将“ $2 A - B$ ”看成“ $2 A + B$ ”，算得结果 $C = 4 a^{2} b - 3 a b^{2} + 4 a b c$ .

(1)、计算 $B$ 的表达式；

(2)、求正确的结果的表达式：

(3)、小强说（2）中的结果的大小与 $c$ 的取值无关，对吗？

查看试题解析
20. 整理一批图书，由一个人做要40小时完成.现计划由一部分人先做4小时，再增加2人和他们一起做8小时，完成这项工作.假设这些人的工作效率相同，具体应先安排多少人工作？

查看试题解析
21. 九年三班的小雨同学想了解本校九年级学生对哪门课程感兴趣，随机抽取了部分九年级学生进行调查（每名学生必只能选择一门课程）．将获得的数据整理绘制如下两幅不完整的统计图．

据统计图提供的信息，解答下列问题：

(1)、在这次调查中一共抽取了名学生，m的值是．

(2)、请根据据以上信息直在答题卡上补全条形统计图；

(3)、扇形统计图中，“数学”所对应的圆心角度数是度；

(4)、若该校九年级共有1000名学生，根据抽样调查的结果，请你估计该校九年级学生中有多少名学生对数学感兴趣．

查看试题解析
22. 合肥天虹商场从厂家批发电视机进行零售，批发价格与零售价格如下表：

电视机型号

甲

乙

批发价（元/台）

1500

2500

零售价（元/台）

2000

3600

若商场购进甲，乙两种型号的电视机共50台，用去9万元．

(1)、求商场购进甲，乙型号的电视机各多少台？

(2)、迎“元旦”商场决定两种型号电视机均打折销售：以零售价的七五折销售乙种型号电视机，两种电视机销售完毕，商场共获利15%，求甲种型号电视机打几折销售？

查看试题解析
23. 如图，点O为直线 $A B$ 上一点，过点O作射线 $O C$ ，使 $∠ B O C$ 的度数比 $∠ A O C$ 度数的2倍还多6°．将一直角三角板 $D F E$ 的直角顶点F放在点O处（注 $∠ D F E = 90 °$ ）．

(1)、如图①，若直角三角板的一边 $F D$ 放在射线 $O A$ 上，求 $∠ C O E$ 的度数；

(2)、如图②，将直角三角板 $F D E$ 绕点O顺时针转动到某位置，若 $O C$ 恰好平分 $∠ A O E$ ，求 $∠ C O D$ 的度数；

(3)、如图③，将直角三角板 $F D E$ 绕点O任意转动，如果 $F D$ 始终在 $∠ A O C$ 的内部，试猜想 $∠ A O D$ 和 $∠ C O E$ 有怎样的数量关系，并说明理由．

查看试题解析

电视机型号	甲	乙
批发价（元/台）	1500	2500
零售价（元/台）	2000	3600