安徽省蚌埠市2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. -21的绝对值是（）

A、-21 B、 $- \frac{1}{21}$ C、 $\frac{1}{21}$ D、21

查看试题解析
2. 已知 $∠ 1$ 和 $∠ 2$ 互补， $∠ 1 = 60 °$ ，则 $∠ 2$ 为（）

A、 $120 °$ B、 $60 °$ C、 $30 °$ D、 $150 °$

查看试题解析
3. 11月10日在沪落幕的第三届进博会各方合作意愿高涨，按一年计，累计意向成交726.2亿美元．其中726.2亿用科学记数法表示为（）

A、 $0.7262 \times 10^{11}$ B、 $7.262 \times 10^{11}$ C、 $726.2 \times 10^{8}$ D、 $7.262 \times 10^{10}$

查看试题解析
4. 我国第七次全国人口普查的标准时点是2020年11月1日零时，普查对象是普查标准时点在中华人民共和国境内的自然人以及在中华人民共和国境外但未定居的中国公民．人口调查采用普查方式的理由是（）

A、人口调查需要获得全面准确的信息 B、人口调查的数目不太大 C、人口调查具有破坏性 D、受条件限制，无法进行抽样调查

查看试题解析
5. 若线段 $A P ， B P ， A B$ 满足 $A P + B P > A B$ ，则关于 $P$ 点的位置，下列说法正确的是（）

A、 $P$ 点一定在直线 $A B$ 上 B、 $P$ 点一定在直线 $A B$ 外 C、 $P$ 点一定在线段 $A B$ 上 D、 $P$ 点一定在线段 $A B$ 外

查看试题解析
6. 为了解某中学2000名学生视力情况，从中随机抽取了500名学生的视力情况进行统计分析，下列说法正确的是（）

A、某中学2000名学生是总体 B、500名学生的视力情况是总体的一个样本 C、样本容量是500名 D、每一名学生是个体

查看试题解析
7. 若 $a^{2} - 3 a = - 1$ ，则代数式 $6 a - 2 a^{2} - 2$ 的值为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 两条长度分别为 $20 cm$ 和 $24 cm$ 的线段有一端点重合，且在一条直线上，则此两条线段的中点之间的距离为（）

A、 $2 cm$ B、 $22 cm$ C、 $2 cm$ 或 $22 cm$ D、 $4 cm$ 或 $20 cm$

查看试题解析
9. 《孙子算经》是中国传统数学的重要著作，其中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根木头的长，绳子还剩余4.5尺；将绳子对折再量木头，则木头还剩余1尺，求木头的长为（）

A、2.5尺 B、3.5尺 C、5.5尺 D、6.5尺

查看试题解析
10. 如图，直线 $A B ， C D$ 相交于点 $O ， ∠ A O C = ∠ B O D$ ， $∠ E O F = ∠ C O G = 90 ° ， O A$ 平分 $∠ C O F$ ，射线 $O D$ 将 $∠ B O E$ 分成了角度数之比为 $2 ： 1$ 的两个角，则 $∠ C O F$ 的大小为（）

A、 $45 °$ B、 $60 °$ C、 $72 °$ 或 $45 °$ D、 $40 °$ 或 $60 °$

查看试题解析

二、填空题

11. 把多项式 $2 x^{3} - 4 x^{2} y + 3 y^{3} - x y^{2}$ 按 $x$ 的升幂排列为．

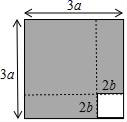
查看试题解析
12. 已知方程 $(m + 2) x^{| m | - 1} - 6 = 0$ 是关于 $x$ 的一元一次方程，则 $m =$ ．

查看试题解析
13. 已知线段 $A B$ ，延长 $A B$ 至点 $C$ ，使 $B C = \frac{2}{3} A B$ ，反向延长 $A B$ 至点 $D$ ，使 $A D = \frac{1}{4} A B$ .若 $A B$ =12 cm，则 $C D$ =cm.

查看试题解析
14. 如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形，若拿掉边长为2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为．

查看试题解析
15. 如图所示，将形状大小完全相同的“ ”按照一定的规律摆成下列图形：第1幅图中“ ”的个数为 $a_{1}$ ，第2幅图中“ ”的个数为 $a_{2}$ ，第3幅图中“ ”的个数为 $a_{3}$ ，…，以此类推．

(1)、按照图中规律， $a_{5} =$ ；

(2)、 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + \dots + \frac{1}{a_{2020}} =$ ．

查看试题解析

三、解答题

16.

(1)、计算： $- {(- 1)}^{2021} + {(- 2)}^{3} \times 3^{2} - 2^{4} \div {(- 4)}^{2}$ ；

(2)、化简： $3 (a^{2} - 2 a b) - (- a b + b^{2}) - 2 b^{2}$ ．

查看试题解析
17.

(1)、解方程 $\frac{x + 3}{2} - \frac{2 x - 1}{3} = 1$ ；

(2)、解方程组： ${\begin{array}{l} 3 x + 4 y = 8 \\ 6 x - 2 y = 11 \end{array}$

查看试题解析
18. 已知： $A = 4 a^{2} b - 3 a b^{2} + 2 a b c$ ， $B = 3 a^{2} b - 2 a b^{2} + a b c$ ．

(1)、计算 $A - 2 B$ 的代数式；

(2)、若单项式 $- 2 x^{1 - 2 a} y^{6}$ 与 $5 x^{2} y^{2 - 4 b}$ 是同类项，求（1）代数式的值．

查看试题解析
19. 某中学为了解七年级学生体能状况，从七年级学生中随机抽取部分学生进行体能测试，测试结果分为 $A ， B ， C ， D$ 四个等级，并依据测试成绩绘制了如下两幅尚不完整的统计图．

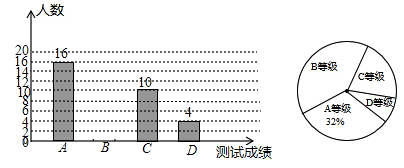(1)、这次抽取的学生的人数是；

(2)、补全条形统计图；

(3)、在扇形统计图中 $C$ 等级所对应的圆心角为度；

(4)、该校七年级学生有800人，请你估计其中 $A$ 等级的学生人数．

查看试题解析
20. 武汉新冠肺炎疫情发生后，全国人民众志成诚抗疫救灾.某公司筹集了抗疫物资120吨打算运往武汉疫区，现有甲、乙、两三种车型供运输选择，每辆车的运载能力和运费如下表所示： (假设每辆车均满载)

车型

甲

乙

丙

运载量（吨/辆）

5

8

10

运费（元/辆）

450

600

700

(1)、全部物资一次性运送可用甲型车8辆，乙型车5辆，丙型车辆.

(2)、若全部物资仅用甲、乙两种车型一次性运完，需运费9600元，求甲、乙两种车型各需多少辆？

(3)、若该公司打算用甲、乙、丙三种车型同时参与运送，已知车辆总数为14辆，且一次性运完所有物资，你能分别求出三种车型的辆数吗？此时的总运费为多少元？

查看试题解析
21. 如图，点 $A ， B$ 在数轴上分别表示有理数 $a ， b$ ，且 $a ， b$ 满足 $| a + 2 | + {(b - 5)}^{2} = 0$ ．

(1)、点 $A$ 表示的数是，点 $B$ 表示的数是．

(2)、若动点 $P$ 从点 $A$ 出发以每秒3个单位长度向右运动，动点 $Q$ 从点 $B$ 出发以每秒1个单位长度向点 $A$ 运动，到达 $A$ 点即停止运动 $P ， Q$ 两点同时出发，且 $Q$ 点停止运动时， $P$ 也随之停止运动，求经过多少秒时， $P ， Q$ 第一次相距3个单位长度？

(3)、在（2）的条件下整个运动过程中，设运动时间为 $t$ 秒，若 $A P$ 的中点为 $M ， B Q$ 的中点为 $N$ ，当 $t$ 为何值时， $B M + A N = 3 P B$ ？

查看试题解析

车型	甲	乙	丙
运载量（吨/辆）	5	8	10
运费（元/辆）	450	600	700