高中数学人教A版(2019) 选修一 第三章 圆锥曲线的方程
试卷更新日期:2021-09-30 类型:单元试卷
一、单选题
-
1. 抛物线 的焦点坐标是( )A、 B、 C、 D、2. 方程 表示双曲线,则实数 的取值范围是( ).A、 B、 或 C、 D、 或3. 椭圆 与椭圆 的( )A、长轴长相等 B、短轴长相等 C、离心率相等 D、焦距相等4. 青花瓷是中华陶瓷烧制工艺的珍品,也是中国瓷器的主流品种之一.如图,是一青花瓷花瓶,其外形上下对称,可看成是双曲线的一部分绕其虚轴旋转所形成的曲面.若该花瓶的瓶口直径为瓶身最小直径的2倍,花瓶恰好能放入与其等高的正方体包装箱内,则双曲线的离心率为( )
 A、 B、 C、 D、5. 已知双曲线 : 的左、右焦点分别为 , ,点 是 的右支上一点, ,连接 与 轴交于点 ,若 ( 为坐标原点),则双曲线 的渐近线方程为( )A、 B、 C、 D、6. 古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆 的中心为原点,焦点 , 均在 轴上, 的面积为 ,过点 的直线交 于点 , ,且 的周长为8.则 的标准方程为( )A、 B、 C、 D、7. 以下四个关于圆锥曲线的命题中
A、 B、 C、 D、5. 已知双曲线 : 的左、右焦点分别为 , ,点 是 的右支上一点, ,连接 与 轴交于点 ,若 ( 为坐标原点),则双曲线 的渐近线方程为( )A、 B、 C、 D、6. 古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆 的中心为原点,焦点 , 均在 轴上, 的面积为 ,过点 的直线交 于点 , ,且 的周长为8.则 的标准方程为( )A、 B、 C、 D、7. 以下四个关于圆锥曲线的命题中①设A.B为两个定点,k为非零常数, ,则动点P的轨迹为双曲线;②曲线 表示焦点在y轴上的椭圆,则 ;③方程 的两根可分别作为椭圆和双曲线的离心率;④双曲 与椭圆 有相同的焦点.其中真命题的序号( )
A、②③④ B、①②③ C、①③④ D、①②④8. 若椭圆 与双曲线 有公共的焦点 , ,点 是两条曲线的交点, ,椭圆的离心率为 ,双曲线的离心率为 ,且 ,则 ( )A、 B、 C、 D、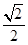
二、多选题
-
9. 点 , 为椭圆 的两个焦点,椭圆 上存在点 ,使得 ,则椭圆 的方程可以是( )A、 B、 C、 D、10. 已知椭圆 的左,右焦点是 是椭圆上一点,若 ,则椭圆的离心率可以是( )A、 B、 C、 D、11. 已知 , 分别为双曲线 的左右焦点, , 分别为其实轴的左右端点,且 ,点 为双曲线右支一点, 为 的内心,则下列结论正确的有( )A、离心率 B、点 的横坐标为定值 C、若 成立,则 D、若 垂直 轴于点 ,则12. 已知曲线 上任意一点到直线 的距离比它到点 的距离大2,则下列结论正确的是( )A、曲线 的方程为 B、若曲线 上的一点 到点 的距离为4,则点 的纵坐标是 C、已知曲线 上的两点 , 到点 的距离之和为10,则线段 的中点横坐标是5 D、已知 , 是曲线 上的动点,则 的最小值为5
三、填空题
-
13. 已知双曲线 的离心率为2,则该双曲线的渐近线方程为14. 已知过抛物线 的焦点 的直线交抛物线于 两点, 是坐标原点, 则 的面积是15. 设椭圆 与双曲线 有公共焦点 , , 是两条曲线的一个公共点,则 等于 .16. 设 分别是椭圆 的两个焦点,点 在椭圆上,若线段 的中点在 轴上,则 =.
四、解答题
-
17. 已知抛物线 : 的焦点与椭圆 : ( )右焦点 重合,且点 在椭圆 上.
(1)、求椭圆 的方程及离心率;(2)、若倾斜角为 的直线 过椭圆 的左焦点 ,且与椭圆相交于 、 两点,求 的面积.18. 已知双曲线 (a>0,b>0)的两条渐近线与抛物线D:y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点,双曲线的离心率为 ,△ABO的面积为2 .(1)、求双曲线C的渐近线方程;(2)、求p的值.19. 已知椭圆 过 两点.(1)、求椭圆 的方程及离心率.(2)、设 为第三象限内一点且在椭圆 上,直线 与 轴交于点 ,直线 与 轴交于点 ,求证:四边形 的面积为定值.20. 已知抛物线 的焦点 与椭圆 的右焦点重合.
(1)、求抛物线 的标准方程;(2)、斜率为 的直线 交抛物线 于不同两点 ,求证: .21. 若椭圆 上有一动点 , 到椭圆 的两焦点 的距离之和等于 ,椭圆 的离心率为 .(1)、求椭圆的方程;(2)、若过点 的直线 与椭圆 交于不同两点 , (0为坐标原点),且 ,求实数 的取值范围.
22. 已知椭圆C1: (a>b>0)的一个顶点与抛物线C2:x2=4y的焦点重合,F1、F2分别是椭圆C1的左、右焦点,C1的离心率e= ,过F2的直线l与椭圆C1交于M,N两点,与抛物线C2交于P,Q两点.(1)、求椭圆C1的方程;(2)、当直线l的斜率k=﹣1时,求△PQF1的面积;(3)、在x轴上是否存在点A, 为常数?若存在,求出点A的坐标和这个常数;若不存在,请说明理由.