河南省驻马店市驿城区2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-29 类型:期中考试
一、单选题
-
1. 下列命题中正确的是( )A、有一组邻边相等的四边形是菱形 B、有一个角是直角的平行四边形是矩形 C、对角线垂直的平行四边形是正方形 D、一组对边平行的四边形是平行四边形2. 已知 是方程 的一个根,则方程的另一个根为( )A、-2 B、2 C、-3 D、33. 观察下列表格,求一元二次方程x2﹣x=1.1的一个近似解是( )
x
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
x2﹣x
0.11
0.24
0.39
0.56
0.75
0.96
1.19
1.44
1.71
A、0.11 B、1.6 C、1.7 D、1.194. 已知关于x的一元二次方程mx2+2x-1=0有两个不相等的实数根,则m的取值范围是( ).A、m>-1且m≠0 B、m<1且m≠0 C、m<-1 D、m>15. 两个相似三角形的相似比为2:3,它们的面积之差为25cm2 , 则较大三角形的面积是( )
A、75cm2 B、65cm2 C、50cm2 D、45cm26. 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFGH是菱形,则四边形ABCD的边需满足的条件是( )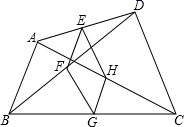 A、AB∥DC B、AC=BD C、AC⊥BD D、AB=DC7. 如图,四边形ABCD中,对角线 ,且 , ,各边中点分别为 、 、 、 ,顺次连接得到四边形 ,再取各边中点 、 、 、 ,顺次连接得到四边形 ,……,依此类推,这样得到四边形 ,则四边形 的面积为( )
A、AB∥DC B、AC=BD C、AC⊥BD D、AB=DC7. 如图,四边形ABCD中,对角线 ,且 , ,各边中点分别为 、 、 、 ,顺次连接得到四边形 ,再取各边中点 、 、 、 ,顺次连接得到四边形 ,……,依此类推,这样得到四边形 ,则四边形 的面积为( )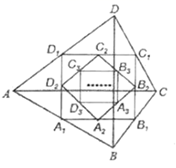 A、 B、 C、 D、不确定
A、 B、 C、 D、不确定二、填空题
-
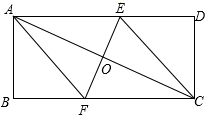
8. 化成一般形式是 , 其中一次项系数是9. 若 ,则 .10. 市政府为了解决市民看病难的问题,决定下调药品的价格.某种药品经过连续两次降价后,由每盒200元下调至128元,求这种药品平均每次降价的百分率是 .11. 如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=
 12. 如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D'落在∠ABC的角平分线上时,DE的长为 .
12. 如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D'落在∠ABC的角平分线上时,DE的长为 .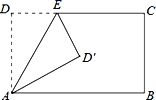
三、解答题
-
13. 解方程(1)、 (用配方法)(2)、 ;14. 如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的格点上.
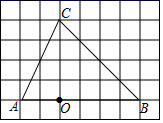 (1)、以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且相似比为1:2;(2)、连接(1)中的BB′,CC′,求四边形BB′C′C的周长.(结果保留根号)15. 某商场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降低0.1元,那么商场平均每天可多售出100张,商场要想平均每天盈利120元,每张贺年卡应降价多少元?16. 已知关于x的一元二次方程(x﹣1)(x﹣4)=p2 , p为实数.(1)、求证:方程有两个不相等的实数根;(2)、p为何值时,方程有整数解.(直接写出三个,不需说明理由)
(1)、以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且相似比为1:2;(2)、连接(1)中的BB′,CC′,求四边形BB′C′C的周长.(结果保留根号)15. 某商场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降低0.1元,那么商场平均每天可多售出100张,商场要想平均每天盈利120元,每张贺年卡应降价多少元?16. 已知关于x的一元二次方程(x﹣1)(x﹣4)=p2 , p为实数.(1)、求证:方程有两个不相等的实数根;(2)、p为何值时,方程有整数解.(直接写出三个,不需说明理由)