河南省驻马店市汝南县2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-29 类型:期中考试
一、单选题
-
1. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 是关于x的一元二次方程 的一个根,则 的值为( )A、2018 B、2020 C、2022 D、20243. 设方程 的两个根为α,β,那么 的值等于( )A、﹣3 B、﹣1 C、1 D、34. 参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )A、 x(x+1)=110 B、 x(x﹣1)=110 C、x(x+1)=110 D、x(x﹣1)=1105. 二次函数y=x2的图象平移后经过点(2,0),则下列平移方法正确的是( )A、向左平移2个单位,向下平移2个单位 B、向左平移1个单位,向上平移2个单位 C、向右平移1个单位,向下平移1个单位 D、向右平移2个单位,向上平移1个单位6. 如图,⊙O是△ABC的外接圆,半径为3cm,若BC=3cm,则∠A的度数为( )
2. 若 是关于x的一元二次方程 的一个根,则 的值为( )A、2018 B、2020 C、2022 D、20243. 设方程 的两个根为α,β,那么 的值等于( )A、﹣3 B、﹣1 C、1 D、34. 参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )A、 x(x+1)=110 B、 x(x﹣1)=110 C、x(x+1)=110 D、x(x﹣1)=1105. 二次函数y=x2的图象平移后经过点(2,0),则下列平移方法正确的是( )A、向左平移2个单位,向下平移2个单位 B、向左平移1个单位,向上平移2个单位 C、向右平移1个单位,向下平移1个单位 D、向右平移2个单位,向上平移1个单位6. 如图,⊙O是△ABC的外接圆,半径为3cm,若BC=3cm,则∠A的度数为( )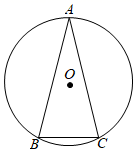 A、30° B、25° C、15° D、10°7. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( )
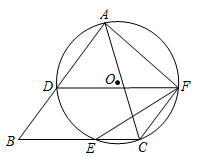
A、30° B、25° C、15° D、10°7. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( ) A、 B、 C、 D、8. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( )
A、 B、 C、 D、8. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( ) A、57° B、52° C、38° D、26°9. 函数y=ax2﹣a与y=ax﹣a(a≠0)在同一坐标系中的图象可能是( )A、
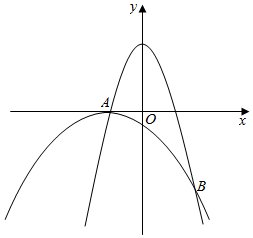
A、57° B、52° C、38° D、26°9. 函数y=ax2﹣a与y=ax﹣a(a≠0)在同一坐标系中的图象可能是( )A、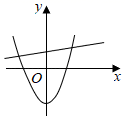 B、
B、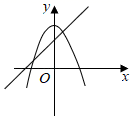 C、
C、 D、
D、 10. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= 且经过点(2,0).下列说法:①abc<0;②4a+2b+c<0;③﹣2b+c=0;④若(﹣ ,y1),( ,y2)是抛物线上的两点,则y1<y2;⑤ b>m(am+b)(其中m≠ ).其中说法正确的是( )
10. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= 且经过点(2,0).下列说法:①abc<0;②4a+2b+c<0;③﹣2b+c=0;④若(﹣ ,y1),( ,y2)是抛物线上的两点,则y1<y2;⑤ b>m(am+b)(其中m≠ ).其中说法正确的是( )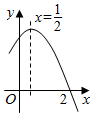 A、①③④⑤ B、①②④ C、①④⑤ D、③④⑤
A、①③④⑤ B、①②④ C、①④⑤ D、③④⑤二、填空题
-
11. 一元二次方程x2﹣2x=0的解是 .
12. 若点M(3,a﹣2),N(b , a)关于原点对称,则ab= .13. 如图,△ABC的内切圆⊙O与BC , CA , AB分别相切于点D , E . F . 且AB=5,AC=12,BC=13,则⊙O的半径是 . 14. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是 .
14. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是 . 15. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点M,N分别在射线 , 上, 长度始终保持不变, , 为 的中点,点D到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .
15. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点M,N分别在射线 , 上, 长度始终保持不变, , 为 的中点,点D到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .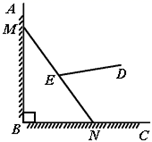
三、解答题
-
16. 已知:关于 的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、当k取最大整数值时,求该方程的解.17. 如图,在平面直角坐标系中, 的三个顶点分别是A(1,3),B(4,4),C(2,1).
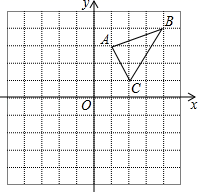
( 1 )把 向左平移4个单位后得到对应的 A1B1C1 , 请画出平移后的 A1B1C1;
( 2 )把 绕原点O旋转180°后得到对应的 A2B2C2 , 请画出旋转后的 A2B2C2;
( 3 )观察图形可知, A1B1C1与 A2B2C2关于点( , )中心对称.
18. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.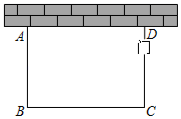 19. 如图,点M, 分别在正方形 的边 , 上,且 ,把 绕点A顺时针旋转 得到 .
19. 如图,点M, 分别在正方形 的边 , 上,且 ,把 绕点A顺时针旋转 得到 .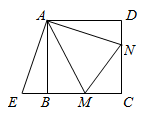 (1)、求证: ≌ .(2)、若 , ,求正方形 的边长.20. 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=NE=3.
(1)、求证: ≌ .(2)、若 , ,求正方形 的边长.20. 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=NE=3. (1)、求证:BC是⊙O的切线;(2)、若AE=4,求⊙O的直径AB的长度.21. 某水果店将标价为10元/斤的某种水果.经过两次降价后,价格为8.1元/斤,并且两次降价的百分率相同.(1)、求该水果每次降价的百分率;(2)、从第二次降价的第1天算起,第x天(x为整数)的销量及储藏和损耗费用的相关信息如下表所示:
(1)、求证:BC是⊙O的切线;(2)、若AE=4,求⊙O的直径AB的长度.21. 某水果店将标价为10元/斤的某种水果.经过两次降价后,价格为8.1元/斤,并且两次降价的百分率相同.(1)、求该水果每次降价的百分率;(2)、从第二次降价的第1天算起,第x天(x为整数)的销量及储藏和损耗费用的相关信息如下表所示:时间(天)
x
销量(斤)
120﹣x
储藏和损耗费用(元)
3x2﹣64x+400
已知该水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<10)之间的函数解析式,并求出第几天时销售利润最大,最大利润是多少?