河南省禹州市2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-29 类型:期中考试
一、单选题
-
1. 下列古钱币图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 抛物线 的顶点坐标是( )A、 B、 C、 D、3. 如图,已知 是⊙O的直径, 是弦,若 ,则 等于( )
2. 抛物线 的顶点坐标是( )A、 B、 C、 D、3. 如图,已知 是⊙O的直径, 是弦,若 ,则 等于( ) A、16° B、24° C、34° D、46°4. 若 是关于x的一元二次方程 的解,则 的值为( )A、2018 B、2019 C、2020 D、20225. 如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )
A、16° B、24° C、34° D、46°4. 若 是关于x的一元二次方程 的解,则 的值为( )A、2018 B、2019 C、2020 D、20225. 如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( ) A、15° B、30° C、45° D、60°6. 若关于x的方程x2﹣2x﹣k=0有实数根,则k的值可能为( )A、﹣4 B、﹣3 C、﹣2 D、07. 如图,⊙O的直径 , 是⊙O的弦, ,垂足为P, ,则 的长为( )
A、15° B、30° C、45° D、60°6. 若关于x的方程x2﹣2x﹣k=0有实数根,则k的值可能为( )A、﹣4 B、﹣3 C、﹣2 D、07. 如图,⊙O的直径 , 是⊙O的弦, ,垂足为P, ,则 的长为( ) A、 B、 C、16 D、88. 函数 与 在同一平面直角坐标系中的图象可能是( )A、
A、 B、 C、16 D、88. 函数 与 在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在平面直角坐标系中,四边形 关于x轴对称, , , ,将四边形 绕点O逆时针旋转90°后得到四边形 ,依此方式,绕点 O连续旋转2021次得到四边形 ,那么点 的坐标是( )
9. 如图,在平面直角坐标系中,四边形 关于x轴对称, , , ,将四边形 绕点O逆时针旋转90°后得到四边形 ,依此方式,绕点 O连续旋转2021次得到四边形 ,那么点 的坐标是( ) A、 B、 C、 D、10. 如图所示的抛物线形构件为某工业园区的新厂房骨架,为了牢固起见,构件需要每隔 加设一根不锈钢的支柱,构件的最高点距底部 ,则该抛物线形构件所需不锈钢支柱的总长度为( )
A、 B、 C、 D、10. 如图所示的抛物线形构件为某工业园区的新厂房骨架,为了牢固起见,构件需要每隔 加设一根不锈钢的支柱,构件的最高点距底部 ,则该抛物线形构件所需不锈钢支柱的总长度为( )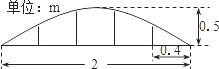 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若一元二次方程 的一个根为 ,则另一个根为.12. 将抛物线 向右平移1个单位长度后经过点 ,则m的值为.13. 某市中学生篮球联赛实行单循环制,参加的每两支球队之间都要进行一场比赛,共要比赛45场,设参加比赛的球队有x支,根据题意,可列方程为.14. 如图,以O为圆心的圆与直线 相交于A,B两点,若 恰为等边三角形,则弧 的长度为.
 15. 如图,在 中,C为直角顶点, ,O为斜边 的中点,将 绕点O逆时针旋转 至 ,当 恰为以 为腰的等腰三角形时, 的值为.
15. 如图,在 中,C为直角顶点, ,O为斜边 的中点,将 绕点O逆时针旋转 至 ,当 恰为以 为腰的等腰三角形时, 的值为.
三、解答题
-
16. 解方程: .17. 如图,在单位长度为1的平面直角坐标系中,已知 的三个顶点的坐标分别为 , , .

( 1 )若 经过平移后得到 ,已知点 的坐标为 ,写出顶点 , 的坐标,并画出 .
( 2 )将 绕点O按逆时针方向旋转90°得到 ,画出 .
( 3 )若 和 关于原点O成中心对称,画出 .
18. 如图,在半圆O中,P是直径 上一动点,且 ,过点P作 交半圆O于点C,连接 ,过点P作 于点D.小明根据学习函数的经验,对线段 , , 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整.对于动点P在 上的不同位置,画图,测量,得到了线段 , , 的长度的几组值,如下表:位置

长度
位置1
位置2
位置3
位置4
位置5
位置6
位置7
位置8
位置9
位置10
0.37
0.88
1.59
2.01
2.44
3.00
3.58
4.37
5.03
5.51
1.45
2.12
2.65
2.83
2.95
3.00
2.95
2.67
2.21
1.65
1.40
1.96
2.27
2.31
2.27
2.13
1.87
1.39
0.89
0.48
在 , , 的长度这三个量中,若确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数.
 (1)、在同一平面直角坐标系 中,分别画出 , 的长度关于 的长度的函数图象.(2)、结合函数图象,解决问题:当 时, 的长度约为 .(精确到 ).19. 地摊经济开放以来,小王以每个40元的价格购进一种玩具,计划以每个60元的价格销售,后来为了尽快回本决定降价销售.已知这种玩具销售量 (个)与每个降价 (元)( )之间满足一次函数关系,其图象如图所示.
(1)、在同一平面直角坐标系 中,分别画出 , 的长度关于 的长度的函数图象.(2)、结合函数图象,解决问题:当 时, 的长度约为 .(精确到 ).19. 地摊经济开放以来,小王以每个40元的价格购进一种玩具,计划以每个60元的价格销售,后来为了尽快回本决定降价销售.已知这种玩具销售量 (个)与每个降价 (元)( )之间满足一次函数关系,其图象如图所示. (1)、求y与x之间的函数解析式.(2)、该玩具每个降价多少元时,小王获利最大?最大利润是多少元?20. 如图,△ABC为⊙O的内接三角形,BC为⊙O的直径,在线段OC上取点D(不与端点重合),作DG⊥BC,分别交AC、圆周于E、F,连接AG,已知AG=EG.
(1)、求y与x之间的函数解析式.(2)、该玩具每个降价多少元时,小王获利最大?最大利润是多少元?20. 如图,△ABC为⊙O的内接三角形,BC为⊙O的直径,在线段OC上取点D(不与端点重合),作DG⊥BC,分别交AC、圆周于E、F,连接AG,已知AG=EG. (1)、求证:AG为⊙O的切线;(2)、已知AG=2,填空:
(1)、求证:AG为⊙O的切线;(2)、已知AG=2,填空:①当四边形ABOF是菱形时,∠AEG=°;
②若OC=2DC,△AGE为等腰直角三角形,则AB=.
21. 阅读材料:各类方程的解法不尽相同,但是它们有一个共同的基本数学思想——转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程 ,通过因式分解可以把它转化为 ,解方程 和 ,可得方程 的解.问题:
(1)、方程 的解是 , , .(2)、求方程 的解.(3)、拓展:用“转化”思想求方程 的解.
22.(1)、问题发现:如图1,已知C为线段 上一点,分别以线段 , 为直角边作等腰直角三角形, , , ,连接 , ,线段 , 之间的数量关系为;位置关系为.
 (2)、拓展探究:
(2)、拓展探究:如图2,把 绕点C逆时针旋转,线段 , 交于点F,则 与 之间的关系是否仍然成立?请说明理由.
 (3)、拓展延伸:
(3)、拓展延伸:如图3,已知 , , ,连接 , , ,把线段 绕点A旋转,若 , ,请直接写出旋转过程中线段 的最大值.
 23. 如图,在平面直角坐标系中,抛物线 交x轴于A,B两点,已知点A的坐标为 , .
23. 如图,在平面直角坐标系中,抛物线 交x轴于A,B两点,已知点A的坐标为 , . (1)、求抛物线的解析式.(2)、D是抛物线位于第三象限的一动点,过点D作y轴的平行线,分别交线段 ,x轴于E,F两点,请问线段 是否存在最大值?若存在,请求出点E的坐标;若不存在,请说明理由,(3)、在抛物线的对称轴上存在点P,使得 ,请直接写出点P的坐标.
(1)、求抛物线的解析式.(2)、D是抛物线位于第三象限的一动点,过点D作y轴的平行线,分别交线段 ,x轴于E,F两点,请问线段 是否存在最大值?若存在,请求出点E的坐标;若不存在,请说明理由,(3)、在抛物线的对称轴上存在点P,使得 ,请直接写出点P的坐标.