河南省三门峡市渑池县2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-29 类型:期中考试
一、单选题
-
1. 一元二次方程 的根的情况是( )A、无实数根 B、有一个实根 C、有两个相等的实数根 D、有两个不相等的实数根2. 下列四个图案中,是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、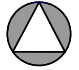 C、
C、 D、
D、 3. 设方程 的两个根为α,β,那么 的值等于( )A、﹣3 B、﹣1 C、1 D、34. 疫情期间,某快递公司推出无接触配送服务,第1周接到5万件订单,第2周到第3周订单量增长率是第1周到第2周订单量增长率的1.5倍,若第3周接到订单为7.8万件,设第1周到第2周的订单增长率为 ,可列得方程为( ).A、 B、 C、 D、5. 如图,A、B、C三点在 上,D是 延长线上的一点, ,那么 的度数为( ).
3. 设方程 的两个根为α,β,那么 的值等于( )A、﹣3 B、﹣1 C、1 D、34. 疫情期间,某快递公司推出无接触配送服务,第1周接到5万件订单,第2周到第3周订单量增长率是第1周到第2周订单量增长率的1.5倍,若第3周接到订单为7.8万件,设第1周到第2周的订单增长率为 ,可列得方程为( ).A、 B、 C、 D、5. 如图,A、B、C三点在 上,D是 延长线上的一点, ,那么 的度数为( ).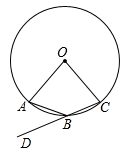 A、80° B、70° C、50° D、40°6. 如图,在⊙O中,直径AB⊥CD,∠A=26°,则∠D度数是( )
A、80° B、70° C、50° D、40°6. 如图,在⊙O中,直径AB⊥CD,∠A=26°,则∠D度数是( ) A、26° B、38° C、52° D、64°7. 对于二次函数 y = -2(x + 3) 的图象,下列说法不正确的是( )A、开口向下 B、对称轴是直线 x = -3 C、顶点坐标为(-3, 0) D、当 x < -3 时,y 随 x 的增大而减小8. 二次函数 的图象如图所示,那么一次函数 的图象大致是( ).
A、26° B、38° C、52° D、64°7. 对于二次函数 y = -2(x + 3) 的图象,下列说法不正确的是( )A、开口向下 B、对称轴是直线 x = -3 C、顶点坐标为(-3, 0) D、当 x < -3 时,y 随 x 的增大而减小8. 二次函数 的图象如图所示,那么一次函数 的图象大致是( ).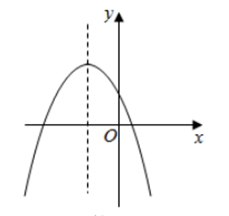 A、
A、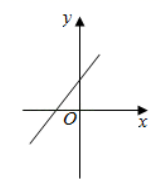 B、
B、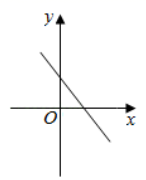 C、
C、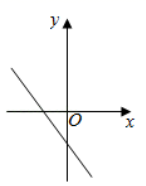 D、
D、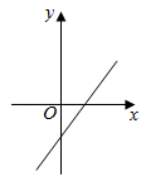 9. 2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作拋物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点 )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点 )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点 )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
9. 2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作拋物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点 )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点 )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点 )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
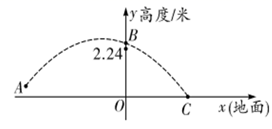 A、 B、 C、 D、10. 如图,在平面直角坐标系中,将正方形 绕点 逆时针旋转45°后得到正方形 ,依此方式,绕点 连续旋转2020次得到正方形 ,如果点 的坐标为(1,0),那么点 的坐标为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,将正方形 绕点 逆时针旋转45°后得到正方形 ,依此方式,绕点 连续旋转2020次得到正方形 ,如果点 的坐标为(1,0),那么点 的坐标为( )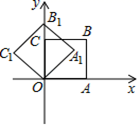 A、(﹣1,1) B、 C、(﹣1,﹣1) D、
A、(﹣1,1) B、 C、(﹣1,﹣1) D、二、填空题
-
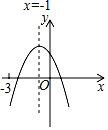
11. 如果一元二次方程 经配方后变为 ,则实数k的值为.12. 关于x的方程kx2﹣4x =0有两个实数根,则k的取值范围是 .13. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2>4ac,②abc<0,③2a+b﹣c>0,④a+b+c<0.其中正确的是.
 14. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .15. 某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是元.
14. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .15. 某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是元.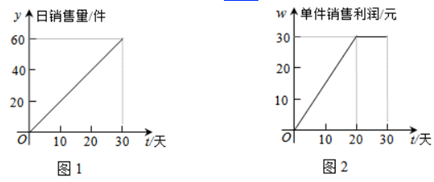
三、解答题
-
16. 用指定的方法解下列方程:(1)、 (配方法)(2)、 (公式法)17. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图 ,点 表示筒车的一个盛水桶.如图 ,当筒车工作时,盛水桶的运行路径是以轴心 为圆心, 为半径的圆,且圆心在水面上方.若圆被水面截得的弦 长为 ,求筒车工作时,盛水桶在水面以下的最大深度.
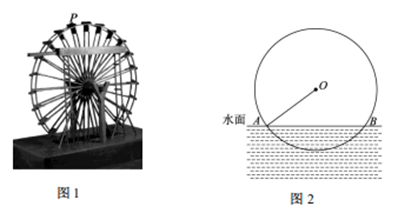 18. 如图,等腰直角 的直角边与正方形 的边长均为 ,边 与边 在同一直线上,点A与点M重合,让 沿 方向以 的速度匀速运动,运动到点A与N重合时停止,设运动的时间为t,运动过程中 与正方形 的重叠部分面积为S,
18. 如图,等腰直角 的直角边与正方形 的边长均为 ,边 与边 在同一直线上,点A与点M重合,让 沿 方向以 的速度匀速运动,运动到点A与N重合时停止,设运动的时间为t,运动过程中 与正方形 的重叠部分面积为S,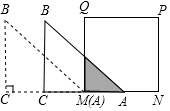 (1)、试写出S关于t的函数关系式,并指出自变量t的取值范围.(2)、当 时,重叠部分的面积是多少?19. 如图,四边形 内接于 , , ,垂足为E.
(1)、试写出S关于t的函数关系式,并指出自变量t的取值范围.(2)、当 时,重叠部分的面积是多少?19. 如图,四边形 内接于 , , ,垂足为E.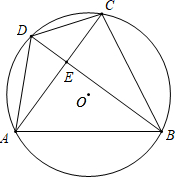 (1)、若 ,求 的度数;(2)、求证: .20. 如图1,有一张长 宽 的长方形硬纸片,裁去角上 个小正方形和 个小长方形(图中阴影部分)之后,恰好折成如图2的有盖纸盒.
(1)、若 ,求 的度数;(2)、求证: .20. 如图1,有一张长 宽 的长方形硬纸片,裁去角上 个小正方形和 个小长方形(图中阴影部分)之后,恰好折成如图2的有盖纸盒.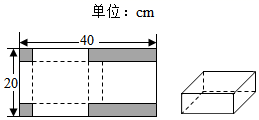 (1)、若纸盒的高是 cm,求纸盒底面长方形的长和宽;(2)、若纸盒的底面积是 ,求纸盒的高.21. 有一家苗圃计划种植桃树和柏树,根据市场调查与预测,种植桃树的利润y1(万元)与投资成本x(万元)满足如图1所示的二次函数y1=ax2;种植柏树的利润y2(万元)与投资成本x(万元)满足如图2所示的正比例函数y2=kx .
(1)、若纸盒的高是 cm,求纸盒底面长方形的长和宽;(2)、若纸盒的底面积是 ,求纸盒的高.21. 有一家苗圃计划种植桃树和柏树,根据市场调查与预测,种植桃树的利润y1(万元)与投资成本x(万元)满足如图1所示的二次函数y1=ax2;种植柏树的利润y2(万元)与投资成本x(万元)满足如图2所示的正比例函数y2=kx .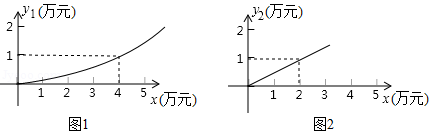 (1)、请分别直接写出利润y1(万元)与利润y2(万元)关于投资成本x(万元)的函数关系式;(2)、若这家苗圃投资4万元种植桃树,投资6万元种植柏树,则可获得的总利润是多少万元?(3)、若这家苗圃种植桃树和柏树投入总成本20万元,且桃树的投资成本不低于2万元,且不高于12万元,则苗圃最少能获得多少总利润?最多可获得多少总利润?22. 如图,在正方形ABCD中,E为CD边上一点,以DE为边向外作正方形DEFG,将正方形DEFG绕点D顺时针旋转,连接AG.
(1)、请分别直接写出利润y1(万元)与利润y2(万元)关于投资成本x(万元)的函数关系式;(2)、若这家苗圃投资4万元种植桃树,投资6万元种植柏树,则可获得的总利润是多少万元?(3)、若这家苗圃种植桃树和柏树投入总成本20万元,且桃树的投资成本不低于2万元,且不高于12万元,则苗圃最少能获得多少总利润?最多可获得多少总利润?22. 如图,在正方形ABCD中,E为CD边上一点,以DE为边向外作正方形DEFG,将正方形DEFG绕点D顺时针旋转,连接AG.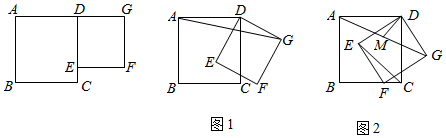 (1)、如图1,若AD=2 、DE=2,当 时,求AG的长;(2)、如图2,正方形DEFG绕点D旋转的过程中,取AG的中点M,连接DM、CE,猜想:DM和CE之间有何等量关系?并利用图2加以证明.23. 在平面直角坐标系中,点O为坐标原点,抛物线y=﹣x2+(k﹣1)x+k(k>0)交x轴的负半轴于点A,交x轴的正半轴于点B,交y轴的正半轴于点C,且AB=4.
(1)、如图1,若AD=2 、DE=2,当 时,求AG的长;(2)、如图2,正方形DEFG绕点D旋转的过程中,取AG的中点M,连接DM、CE,猜想:DM和CE之间有何等量关系?并利用图2加以证明.23. 在平面直角坐标系中,点O为坐标原点,抛物线y=﹣x2+(k﹣1)x+k(k>0)交x轴的负半轴于点A,交x轴的正半轴于点B,交y轴的正半轴于点C,且AB=4. (1)、如图1,求k的值;(2)、如图2,点D在第一象限的抛物线上,点E在线段BC上,DE//y轴,若DE= BE,求点D的坐标;(3)、如图3,在(2)的条件下,F为抛物线顶点,点P在第四象限的抛物线上,FP交直线DE于点Q,点G与点D关于y轴对称,若GQ=DP,求点P的坐标.
(1)、如图1,求k的值;(2)、如图2,点D在第一象限的抛物线上,点E在线段BC上,DE//y轴,若DE= BE,求点D的坐标;(3)、如图3,在(2)的条件下,F为抛物线顶点,点P在第四象限的抛物线上,FP交直线DE于点Q,点G与点D关于y轴对称,若GQ=DP,求点P的坐标.