河南省平顶山市叶县2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-29 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $(a - 1) x^{2} + b x + c = 0$ 是关于x的一元二次方程，则（）

A、 $a \neq 1$ B、 $a = 1$ C、 $a \neq - 1$ D、 $a \neq 0$ 且 $b \neq 0$

查看试题解析
2. 如图，直线a∥b∥c，直线m、n与这三条平行线分别交于点A、B、C和点D、E、F．若AB＝3，BC＝5，DF＝12，则DE的值为（）

A、 $\frac{9}{4}$ B、4 C、 $\frac{9}{2}$ D、 $\frac{15}{2}$

查看试题解析
3. 下列一元二次方程没有实数根的是（）

A、 $x^{2} + 2 x + 1 = 0$ B、 $x^{2} + x + 2 = 0$ C、 $x^{2} - 1 = 0$ D、 $x^{2} - 2 x - 1 = 0$

查看试题解析
4. 某厂家2020年1～5月份的口罩产量统计如图所示.设从2月份到4月份，该厂家口罩产量的平均月增长率为x，根据题意可得方程（　　）

A、180（1﹣x）²=461 B、180（1+x）²=461 C、368（1﹣x）²=442 D、368（1+x）²=442

查看试题解析
5. 如图，在 $△ A B C$ 中，点D、E分别在边 $A B$ 、 $A C$ 上，则在下列五个条件中：① $∠ A E D = ∠ B$ ；② $D E // B C$ ；③ $\frac{A D}{A C} = \frac{A E}{A B}$ ；④ $A D \cdot B C = D E \cdot A C$ ，能满足 $△ A D E \sim △ A C B$ 的条件有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图①所示，平整的地面上有一个不规则图案（图中阴影部分），小明想了解该图案的面积是多少，他采取了以下办法：用一个长为 $5m$ ，宽为 $4m$ 的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计实验结果），他将若干次有效实验的结果绘制成了②所示的折线统计图，由此他估计不规则图案的面积大约为（）

A、 ${6m}^{2}$ B、 ${7m}^{2}$ C、 ${8m}^{2}$ D、 ${9m}^{2}$

查看试题解析
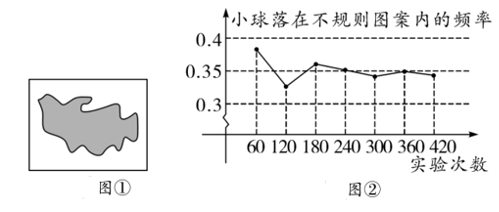7. 如图，菱形ABCD的对角线相交于点O ， AC＝12，BD＝16，点P为边BC上一点，且点P不与点B、C重合．过点P作PE⊥AC于点E ， PF⊥BD于点F ，连结EF ，则EF的最小值为（）

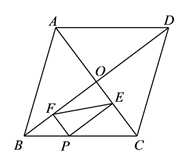A、4 B、4.8 C、5 D、6

查看试题解析
8. 图2是图1中长方体的三视图，若用S表示面积，S_主＝x²+2x ， S_左＝x²+x ，则S_俯＝（）

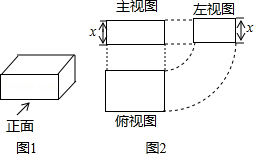A、x²+3x+2 B、x²+2 C、x²+2x+1 D、2x²+3x

查看试题解析
9. 矩形ABCD与CEFG，如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH．若BC=EF=2，CD=CE=1，则GH=（）

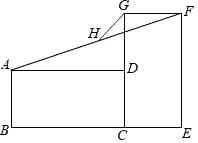A、1 B、 $\frac{2}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析
10. 宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ （约0.618）的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，给我们以协调和匀称的美感．我们可以用这样的方法画出黄金矩形：作正方形ABCD，分别取AD、BC的中点E、F，连接EF：以点F为圆心，以FD为半径画弧，交BC的延长线于点G；作GH⊥AD，交AD的延长线于点H，则图中下列矩形是黄金矩形的是（　　）

A、矩形ABFE B、矩形EFCD C、矩形EFGH D、矩形DCGH

查看试题解析

二、填空题

11. 一元二次方程 $4 x (x - 2) = x - 2$ 的解为．

查看试题解析
12. 在做“抛掷一枚质地均匀的硬币”试验时，下列说法正确的是.
①不同次数的试验，正面向上的频率可能会不相同

②当抛掷的次数 $n$ 很大时，正面向上的次数一定为 $\frac{n}{2}$

③多次重复试验中，正面向上发生的频率会在某个常数附近摆动，并趋于稳定

④连续抛掷 $5$ 次硬币都是正面向上，第 $6$ 次抛掷出现正面向上的概率小于 $\frac{1}{2}$

查看试题解析
13. 如图，在平面直角坐标系中，已知点A（﹣3，6），B（﹣9，﹣3），以原点O为位似中心，相似比为 $\frac{1}{3}$ ，把△ABO缩小，则点A的对应点A′的坐标是.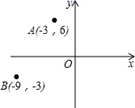

查看试题解析
14. 一个几何体由n个大小相同的小立方块搭成，其从左面、上面看到的形状图如图所示，则n的最小值是.

查看试题解析
15. 如图，在正方形纸片 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于点O，折叠正方形纸片 $A B C D$ ，使 $A D$ 落在 $B D$ 上，点A恰好与 $B D$ 上的点F重合，展开后，折痕 $D E$ 分别交 $A B$ 、 $A C$ 于点E，G，连接 $G F$ ，下列结论中正确的是. （填序号）

① $∠ A G E = 67.5 °$ ；②四边形 $A E F G$ 是菱形；③ $B E = 2 O F$ ；④ $S_{△ D O G} ： S_{四边形 O G E F} = \sqrt{2} ： 1$ .

查看试题解析

三、解答题

16. 解方程

(1)、 $4 x^{2} - 3 x = 18$ （用配方法）

(2)、 $(y - 2) (3 y - 5) = 1$ （用公式法）

(3)、 $2 x^{2} + 4 x = x + 2$ （用适当的方法）

查看试题解析
17. 一个边长为 $2 cm$ 的大正方体上挖去一个小正方体（边长是大正方体的一半），得到的几何体如图所示，请画出它的三视图（比例为1：1）

查看试题解析
18. $2020$ 年国家提出并部署了“新基建”项目，主要包含“特高压，城际高速铁路和城市轨道交通， $5 G$ 基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩”等.《 $2020$ 新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域（ $5 G$ 基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩）总体的人才与就业机会.下图是其中的一个统计图.
请根据图中信息，解答下列问题：

(1)、填空：图中 $2020$ 年“新基建”七大领域预计投资规模的中位数是亿元；

(2)、甲，乙两位待业人员，仅根据上面统计图中的数据，从五大细分领域中分别选择了“ $5 G$ 基站建设”和“人工智能”作为自己的就业方向，请简要说明他们选择就业方向的理由各是什么；

查看试题解析
19. 如图，在Rt△ABC中，∠C=90°，AC=8m，BC=6m，点P由C点出发以2m/s的速度向终点A匀速移动，同时点Q由点B出发以1m/s的速度向终点C匀速移动，当一个点到达终点时另一个点也随之停止移动．

(1)、经过几秒△PCQ的面积为△ACB的面积的 $\frac{1}{3}$ ？

(2)、经过几秒，△PCQ与△ACB相似？

查看试题解析
20. 某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“六一”儿童节，商店决定采取适当的降价措施，以扩大销售量增加利润，经市场调查发现，如果每件童装降价1元，那么平均可多售出2件．

(1)、每件童装降价多少元时，能让利于顾客并且商家平均每天能赢利1200元．

(2)、要想平均每天赢利2000元，可能吗？请说明理由．

查看试题解析
21. 如图，在矩形ABCD中，AB＝3cm，BC＝6cm.点P从点D出发向点A运动，运动到点A即停止；同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.

(1)、当t为何值时，四边形ABQP是矩形，请说明理由；

(2)、当t为何值时，四边形AQCP是菱形，请说明理由；

(3)、直接写出（2）中菱形AQCP的周长和面积，周长是cm，面积是cm².

查看试题解析
22. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度．

(1)、如图1所示，淇淇将镜子放在地面上，然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E ，测得脚掌中心位置B到镜面中心C的距离是50cm ，镜面中心C距离旗杆底部D的距离为4m ，已知淇淇同的身高是1.54m ，眼睛位置A距离淇淇头顶的距离是4cm ，求旗杆DE 的高度．

(2)、如图2所示，嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米，在同时刻测量旗杆的影长时，旗杆的影子一部分落在地面上（BC），另一部分落在斜坡上（CD），他测得落在地面上的影长为10米，落在斜坡上的影长为 $2 \sqrt{2}$ 米，∠DCE=45°，求旗杆AB的高度？

查看试题解析
23. 背景：一次小组合作探究课上，小明将两个正方形按背景图位置摆放（点E，A，D在同一条直线上），发现BE=DG且BE⊥DG．小组讨论后，提出了三个问题，请你帮助解答：

(1)、将正方形AEFG绕点A按逆时针方向旋转，（如图1）还能得到BE=DG吗？如果能，请给出证明．如若不能，请说明理由：

(2)、把背景中的正方形分别改为菱形AEFG和菱形ABCD，将菱形AEFG绕点A按顺时针方向旋转，（如图2）试问当∠EAG与∠BAD的大小满足怎样的关系时，背景中的结论BE=DG仍成立？请说明理由；

(3)、把背景中的正方形改成矩形AEFG和矩形ABCD，且 $\frac{A E}{A G} = \frac{A B}{A D} = \frac{2}{3}$ ，AE=4，AB=8，将矩形AEFG绕点A按顺时针方向旋转（如图3），连接DE，BG．小组发现：在旋转过程中， BG²+DE²是定值，请求出这个定值．

查看试题解析