河南省平顶山市郏县2019-2020学年九年级下学期数学期中考试试卷
试卷更新日期:2021-09-29 类型:期中考试
一、单选题
-
1. 四个实数0、 、﹣3.14、﹣2中,最小的数是( )A、0 B、 C、﹣3.14 D、﹣22. 下列计算错误的是( )A、 B、 C、 D、3. 华为Mate 30 5G系列是近期相当火爆的5G国产手机,它采用的麒麟990 5G芯片在指甲盖大小的尺寸上集成了103亿个晶体管,将103亿用科学记数法表示为( )A、1.03×109 B、10.3×109 C、1.03×1010 D、1.03×10114. 如图所示的工件,其俯视图是( )
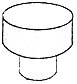 A、
A、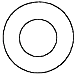 B、
B、 C、
C、 D、
D、 5. 下列说法正确的是( )A、四个数2、3、5、4的中位数为4 B、想了解郏县初三学生备战中考复习情况,应采用普查 C、一组数据的方差越大,则这组数据的波动也越大 D、从初三体考成绩中抽取100名学生的体考成绩,这100名考生是总体的一个样本6. 不等式组 的解集在数轴上表示正确的是( )A、
5. 下列说法正确的是( )A、四个数2、3、5、4的中位数为4 B、想了解郏县初三学生备战中考复习情况,应采用普查 C、一组数据的方差越大,则这组数据的波动也越大 D、从初三体考成绩中抽取100名学生的体考成绩,这100名考生是总体的一个样本6. 不等式组 的解集在数轴上表示正确的是( )A、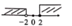 B、
B、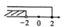 C、
C、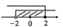 D、
D、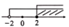 7. 如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0, ),分别以A,B为圆心,大于 AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
7. 如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0, ),分别以A,B为圆心,大于 AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )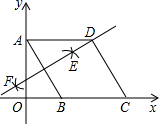 A、(2,2) B、(2, ) C、( ,2) D、( +1,8. 我国古代数学名著《孙子算经》中记载了一道题,大意是:有100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )A、 B、 C、 D、9. 直线y= x+4与x轴、y轴分别交于点A和点B , 点C , D分别为线段AB , OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( ).
A、(2,2) B、(2, ) C、( ,2) D、( +1,8. 我国古代数学名著《孙子算经》中记载了一道题,大意是:有100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )A、 B、 C、 D、9. 直线y= x+4与x轴、y轴分别交于点A和点B , 点C , D分别为线段AB , OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( ).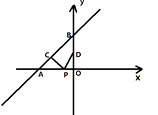 A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)10. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)10. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( ) A、
A、 B、
B、 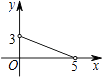 C、
C、 D、
D、
二、填空题
-
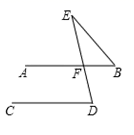
11. 计算 的结果是.12. 如图AB∥CD,AB与DE交于点F,∠B=40°,∠D=70°,则∠E=.
 13. 已知关于x的一元二次方程 有两个不相等的实数根,则a的取值范是.14. 如图,在矩形 中, , ,以点B为圆心, 的长为半径作 交 于点E;以点A为圆心, 的长为半径作 交 于点F,则图中阴影部分的面积为.
13. 已知关于x的一元二次方程 有两个不相等的实数根,则a的取值范是.14. 如图,在矩形 中, , ,以点B为圆心, 的长为半径作 交 于点E;以点A为圆心, 的长为半径作 交 于点F,则图中阴影部分的面积为.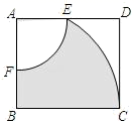 15. 如图,在矩形ABMN中,AN=1,点C是MN的中点,分别连接AC,BC,且BC=2,点D为AC的中点,点E为边AB上一个动点,连接DE,点A关于直线DE的对称点为点F,分别连接DF,EF.当EF⊥AC时,AE的长为.
15. 如图,在矩形ABMN中,AN=1,点C是MN的中点,分别连接AC,BC,且BC=2,点D为AC的中点,点E为边AB上一个动点,连接DE,点A关于直线DE的对称点为点F,分别连接DF,EF.当EF⊥AC时,AE的长为.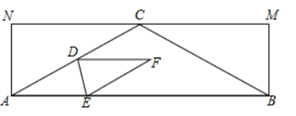
三、解答题
-
16. 先化简再求值:
,其中,x为该不等组 的整数解.
17. 中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题: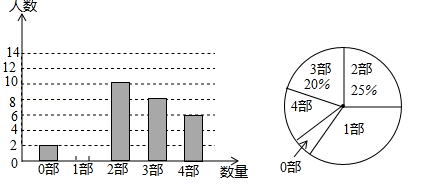 (1)、本次调查所得数据的众数是部,中位数是部,扇形统计图中“1部”所在扇形的圆心角为度.(2)、请将条形统计图补充完整;(3)、没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为.18. 如图,反比例函数 的图象经过格点(网格线的交点)A,作 轴于点C.
(1)、本次调查所得数据的众数是部,中位数是部,扇形统计图中“1部”所在扇形的圆心角为度.(2)、请将条形统计图补充完整;(3)、没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为.18. 如图,反比例函数 的图象经过格点(网格线的交点)A,作 轴于点C.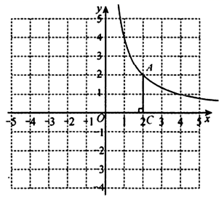 (1)、求反比例函数的解析式;(2)、直线 经过格点A交x轴于点B.记 (不含边界)围成区域W.
(1)、求反比例函数的解析式;(2)、直线 经过格点A交x轴于点B.记 (不含边界)围成区域W.①当直线AB经过格点(0,1)时,区域W内的格点坐标是 ;
②若区域W内恰有1个格点,结合函数图象,直接写出正数k的取值范围.
19. 如图,在△ABC中,∠BAC=90°,点O在BC上,以线段OC的长为半径的⊙O与AB相切于点D,分别交BC、AC于点E、F,连接ED并延长,交CA的延长线于点G.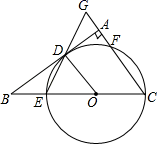 (1)、求证:∠DOC=2∠G.(2)、已知⊙O的半径为3.
(1)、求证:∠DOC=2∠G.(2)、已知⊙O的半径为3.①若BE=2,则DA=.
②当BE= 时,四边形DOCF为菱形.
20. 某地的一座人行天桥如图所示,天桥高为6米,坡面 的坡度为 ,文化墙 在天桥底部正前方8米处( 的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为 .(参考数据: , )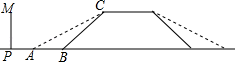 (1)、若新坡面坡角为 ,求坡角 度数;(2)、有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙 是否需要拆除?请说明理由.21. 某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)、若新坡面坡角为 ,求坡角 度数;(2)、有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙 是否需要拆除?请说明理由.21. 某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.时间x(天)
1≤x<9
9≤x<15
售价(元/斤)
第1次降价后的价格
第2次降价后的价格
销量(斤)
80-3x
120-x
储存消耗费用(元)
40+3x
3x2-64x+400
(1)、求该种水果每次降价的百分率;(2)、从第一次降价的第1天算起,第x天(x为整数)的售价、销量的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x( )之间的函数关系式,并求出第几天时销售利润最大?22. 问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,记△ADM的面积为S1 , △BND的面积为S2.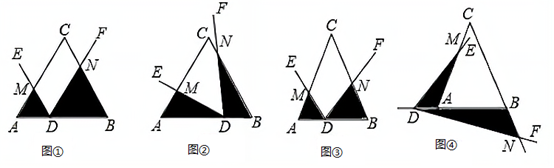 (1)、初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1S2=;(2)、类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1S2的值;(3)、延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.
(1)、初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1S2=;(2)、类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1S2的值;(3)、延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.(Ⅰ)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1S2的表达式(结果用a,b和α的三角函数表示).
(Ⅱ)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1S2的表达式,不必写出解答过程.
23. 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( , )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C. (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)、求△PAC为直角三角形时点P的坐标.