河南省南阳市镇平县2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{18}$ B、 $\sqrt{13}$ C、 $\sqrt{27}$ D、 $\sqrt{12}$

查看试题解析
2. 一元二次方程x²﹣8x+20=0的根的情况是（　　）

A、没有实数根 B、有两个相等的实数根 C、只有一个实数根 D、有两个不相等的实数根

查看试题解析
3. 一个多边形的边长为2，3，4，5，6，另一个和它相似的多边形的最长边为24，则这个多边形的最短边长为（）

A、6 B、8 C、12 D、10

查看试题解析
4. 用配方法解方程 $2 x^{2} - x - 1 = 0$ ，变形结果正确的是（）

A、 ${(x - \frac{1}{2})}^{2} = \frac{3}{4}$ B、 ${(x - \frac{1}{4})}^{2} = \frac{3}{4}$ C、 ${(x - \frac{1}{4})}^{2} = \frac{17}{16}$ D、 ${(x - \frac{1}{4})}^{2} = \frac{9}{16}$

查看试题解析
5. 如图，线段CD两个端点的坐标分别为C(4，4)，D(6，2)，以原点O为位似中心，在第一象限内将线段CD缩小为原来的一半后得到线段AB，则端点A的坐标为（）

A、(2，2) B、(3，3) C、(3，1) D、(4，1)

查看试题解析
6. 近几年，手机支付用户规模增长迅速，据统计2016年手机支付用户约为4.69亿人，连续两年增长后，2018年手机支付用户达到约5.83亿人，如果设这两年手机支付用户的年均增长率为x，则根据题意可以列出方程为（）

A、4.69（1+x）＝5.83 B、4.69（1+2x）＝5.83 C、4.69（1+x）²＝5.83 D、4.69（1﹣x）²＝5.83

查看试题解析
7. 已知，一个小球由桌面沿着斜坡向上前进了10cm，此时小球距离桌面的高度为5cm，则这个斜坡的坡度i为（）

A、2 B、1：2 C、1： $\sqrt{2}$ D、1： $\sqrt{3}$

查看试题解析
8. 比较大小错误的是（）

A、 $\sqrt{5}$ ＜ $\sqrt{7}$ B、 $\sqrt{35}$ +2＜ $\sqrt{82}$ ﹣1 C、 $\frac{- 7 - \sqrt{23}}{2}$ ＞﹣6 D、 $2 \sqrt{3}$ ＞ $3 \sqrt{2}$

查看试题解析
9. 如图，在 $△ A B C$ 中，点D，E分别在 $A C$ ， $A B$ 上且 $D E / / B C$ ，若 $S_{△ A D E} ： S_{△ B D E} = 2 ： 3$ ，则 $S_{△ A D E} ： S_{△ A C B} = ($ $)$

A、2：3 B、4：9 C、4：25 D、4：19

查看试题解析
10. 如图，已知点E是矩形ABCD的对角线AC上的一动点，正方形EFGH的顶点G、H都在边AD上，若AB=3，BC=4，则tan∠AFE的值（）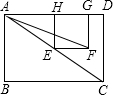

A、等于 $\frac{3}{7}$ B、等于 $\frac{\sqrt{3}}{3}$ C、等于 $\frac{3}{4}$ D、随点E位置的变化而变化

查看试题解析

二、填空题

11. 将方程2x²=1-3x化为一般形式是．

查看试题解析
12. 比例尺为1∶4000000的地图上，两城市间的图上距离为3cm，则这两城市间的实际距离为km.

查看试题解析
13. 满足﹣ $\sqrt{3}$ ＜x＜ $\sqrt{6}$ 的所有整数x的和是.

查看试题解析
14. 如图，河宽CD为100 $\sqrt{3}$ 米，在C处测得对岸A点在C点南偏西30°方向、对岸B点在C点南偏东45°方向，则A、B两点间的距离是米.（结果保留根号）

查看试题解析
15. 将三角形纸片(△ABC)按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF.已知AB＝AC＝3，BC＝4，若以点B′，F，C为顶点的三角形与△ABC相似，则BF的长度是.

查看试题解析

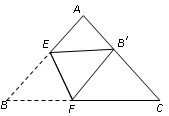
三、解答题

16. 计算： $\sqrt[3]{- 27} + \sqrt{81} - \sqrt{2 + \frac{1}{4}} + \sqrt{5} \times (1 + \frac{1}{\sqrt{5}})$ .

查看试题解析
17. 解下列方程；

(1)、4x²﹣121＝0；

(2)、2x（x﹣1）+6＝2（0.5x+3）；

(3)、4x²﹣8x﹣1＝0.

查看试题解析
18. 如图，已知矩形ABCD的顶点A，D分别落在x轴、y轴上，OD＝2OA＝6，AD：AB＝3：1，CE垂直y轴于点E.

(1)、求证： $△ C D E ∽ △ D A O$ ；

(2)、直接写出点B和点C的坐标.

查看试题解析
19. 黄河，既是一条源远流长、波澜壮阔的自然河，又是一条孕育中华民族灿烂文明的母亲河，数学课外实践活动中，小林和同学们在黄河南岸小路上的A，B两点处，用测角仪分别对北岸的观景亭D进行测量.如图，测得∠DAC＝45°，∠DBC＝65°.若AB＝200米，求观景亭D到小路AC的距离约为多少米？（结果精确到1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）

查看试题解析
20. 关于 $x$ 的一元二次方程 $(m - 2) x^{2} + 2 m x + m + 3 = 0$ 有两个不相等的实数根.

(1)、求 $m$ 的取值范围；

(2)、当 $m$ 取满足条件的最大整数时，求方程的根.

查看试题解析
21.

(1)、问题情境：如图1，Rt $△ A B C$ 中，∠ACB＝90°，CD⊥AB，我们可以利用 $△ A B C$ 与 $△ A C D$ 相似证明AC²＝AD•AB，这个结论我们称之为射影定理，试证明这个定理.

(2)、结论运用：如图2，正方形ABCD的边长为6，点O是对角线AC，BD的交点，点E在CD上，过点C作CF⊥BE，垂足为F，连接OF，试利用射影定理证明 $△ B O F ∽ △ B E D$ .

查看试题解析
22. 位于河南省登封市境内的元代观星台，是中国现存最早的天文台，也是世界文化遗产之一．某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度．如图所示，他们在地面一条水平步道MP上架设测角仪，先在点M处测得观星台最高点A的仰角为22°，然后沿MP方向前进16m到达点N处，测得点A的仰角为45°．测角仪的高度为1.6m求观星台最高点A距离地面的高度（结果精确到0.1m．参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40， $\sqrt{2}$ ≈1.41）．

查看试题解析
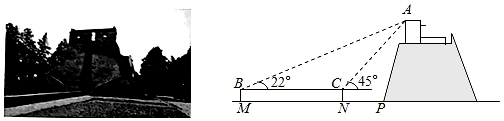23. 如图1，在Rt $△ A B C$ 中，∠B＝90°，AB＝4，BC＝2，点D，E分别是边BC，AC的中点，连接DE.将 $△ C D E$ 绕点C逆时针方向旋转，记旋转角为α.

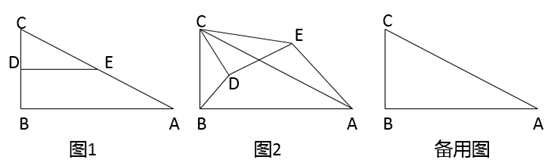(1)、问题发现
①当α＝0°时， $\frac{A E}{B D}$ ＝；

②当α＝180°时， $\frac{A E}{B D}$ ＝；

(2)、拓展探究
试判断当0°＜α＜360°时， $\frac{A E}{B D}$ 的大小有无变化？请仅就图2的情形给出证明；

(3)、问题解决
当 $△ C D E$ 绕点C逆时针旋转至A，B，E三点在同一条直线上时，求线段BD的长.

查看试题解析