河南省南阳市宛城区2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-29 类型:期中考试
一、单选题
-
1. 若式子 有意义,则实数x的值可以是( )A、0 B、1 C、2 D、52. 已知= , 则的值是( )A、 B、 C、 D、3. 下列二次根式中,不能与 合并的是( )A、 B、 C、 D、4. 关于x的一元二次方程x2+(k﹣2)x+k2﹣1=0的一个根是0,则k的值是( )A、1 B、﹣1 C、±1 D、25. 从“+,﹣,×,÷”中选择一种运算符号,填入算式“( +1)□x”的“□”中,使其运算结果为有理数,则实数x不可能是( )A、 +1 B、5 ﹣1 C、 ﹣2 D、1﹣6. 若 ,则 的值为( )A、10 +1 B、10 C、﹣13 D、17. 定义新运算“a※b”:对于任意实数a、b,都有a※b=(a+b)(a﹣b)﹣1,例4※2=(4+2)(4﹣2)﹣1=12﹣1=11.则方程x※1=x的根的情况为( )A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、只有一个实数根8. 某口罩加工厂 年一月份口罩产值达 万元,第一季度总产值达 万元,若第二、三月份的月平均增长率为x,则由题意可列方程为( )A、 B、 C、 D、9. 等腰三角形的一边长为4,另外两边的长是关于x的方程 的两个实数根,则该等腰三角形的周长是( )A、14 B、14或15 C、4或6 D、24或2510. 如图,矩形ABCD的顶点A、C分别在x、y轴的正半轴上,点D(﹣2,3),AD=5,若反比例函数y= (x>0)的图象经过点B,则k的值为( )
 A、4 B、 C、10 D、
A、4 B、 C、10 D、二、填空题
-
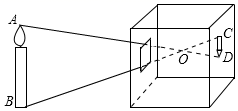
11. 方程x(x﹣2)=2﹣x的根是.12. 如图是小孔成像原理示意图,若点O到AB的距离是18cm,O到CD的距离是6cm,物体AB的高度是9cm,则像CD的高度是cm.
 13. 已知M= ﹣x+3,当x分别取1,2,3,…,2020时,所对应M值的总和是.14. “黄金分割”被视为最美丽的几何学比率,在建筑、艺术和日常生活中处处可见.如图,D、E是△ABC中边BC的两个“黄金分割”点,则△ADE与△ABC的面积之比是.
13. 已知M= ﹣x+3,当x分别取1,2,3,…,2020时,所对应M值的总和是.14. “黄金分割”被视为最美丽的几何学比率,在建筑、艺术和日常生活中处处可见.如图,D、E是△ABC中边BC的两个“黄金分割”点,则△ADE与△ABC的面积之比是.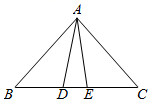 15. 如图,A、B、C、D都是格点(小正方形的顶点),动点E在线段AC上,若点A的坐标是(1,1),则当△ADE与△ABC相似时,动点E的坐标是.
15. 如图,A、B、C、D都是格点(小正方形的顶点),动点E在线段AC上,若点A的坐标是(1,1),则当△ADE与△ABC相似时,动点E的坐标是.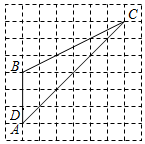
三、解答题
-
16. 解方程: x2﹣4x﹣ =0.17. 计算:(1)、 ;(2)、 .18. 求当m为何值时,关于x的方程mx2﹣(2m﹣1)x+m﹣2=0有实数根.19. 如图,E是▱ABCD的边CD延长线上一点,连接BE,交AC于点O,交AD于F.
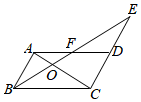 (1)、图中的相似三角形共有 .A、7对; B、6对; C、5对; D、4对.(2)、求证:OB2=OE•OF.20. “通过等价变换,化复杂为简单,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式.例如:解方程x﹣ =0,就可利用该思维方式,设 =y,将原方程转化为: 这个熟悉的关于y的一元二次方程,解出y,再求x.这种方法又叫“换元法”.请你用这种思维方式和换元法解决下列问题:(1)、填空:若 ,则 的值为;(2)、直接写出方程 的根;(3)、解方程: 2 ﹣8=0.21. (教材呈现)如图是华师版九年级上册数学教材第77页的部分内容.
(1)、图中的相似三角形共有 .A、7对; B、6对; C、5对; D、4对.(2)、求证:OB2=OE•OF.20. “通过等价变换,化复杂为简单,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式.例如:解方程x﹣ =0,就可利用该思维方式,设 =y,将原方程转化为: 这个熟悉的关于y的一元二次方程,解出y,再求x.这种方法又叫“换元法”.请你用这种思维方式和换元法解决下列问题:(1)、填空:若 ,则 的值为;(2)、直接写出方程 的根;(3)、解方程: 2 ﹣8=0.21. (教材呈现)如图是华师版九年级上册数学教材第77页的部分内容.
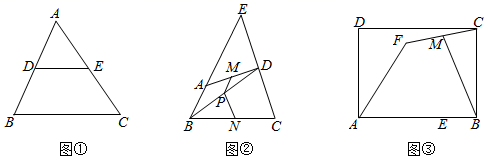 (1)、(定理证明)请根据教材内容,结合图①,写出证明过程.(2)、(定理应用)如图②,四边形ABCD中,M、N、P分别为AD、BC、BD的中点,边BA、CD延长线交于点E,∠E=45°,则∠MPN的度数是.(3)、如图③,矩形ABCD中,AB=4,AD=3,点E在边AB上,且AE=3BE.将线段AE绕点A旋转一周,得到线段AF,M是线段CF的中点,直接写出旋转过程中线段BM长的最大值和最小值.22. (问题提出)在2020抗击新冠肺炎的斗争中,某中学响应政府“停课不停学”的号召进行线上学习,九年级一班的全体同学在自主完成学习任务的同时,全班每两个同学都通过一次视频电话,彼此关怀,互相勉励,共同提高,若每两名同学之间仅通过一次视频电话,如何求全班56名同学共通过多少次电话呢?
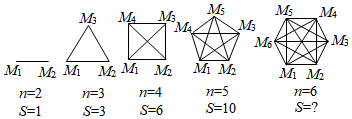
(1)、(定理证明)请根据教材内容,结合图①,写出证明过程.(2)、(定理应用)如图②,四边形ABCD中,M、N、P分别为AD、BC、BD的中点,边BA、CD延长线交于点E,∠E=45°,则∠MPN的度数是.(3)、如图③,矩形ABCD中,AB=4,AD=3,点E在边AB上,且AE=3BE.将线段AE绕点A旋转一周,得到线段AF,M是线段CF的中点,直接写出旋转过程中线段BM长的最大值和最小值.22. (问题提出)在2020抗击新冠肺炎的斗争中,某中学响应政府“停课不停学”的号召进行线上学习,九年级一班的全体同学在自主完成学习任务的同时,全班每两个同学都通过一次视频电话,彼此关怀,互相勉励,共同提高,若每两名同学之间仅通过一次视频电话,如何求全班56名同学共通过多少次电话呢?(模型构建)用点 、 、 、…、 分别表示第1、2、3、…、56名同学,把该班级人数n与视频通话次数S之间的关系用如图模型表示:
(问题解决)
(1)、填写如图中第5个图中S的值为.(2)、通过探索发现,通电话次数S与该班级人数n之间的关系式为 , 则当n=56时,对应的S=.(3)、若该班全体女生相互之间共通话253次,求该班共有多少名女生?(4)、若该班数学兴趣小组的同学们,每两位同学之间互发一条微信问候,小明统计全组共发送微信182条,则该班数学兴趣小组的人数是.23.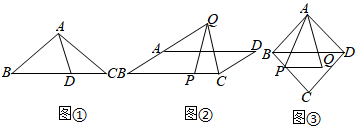 (1)、(证明)如图①,在△ABC中,D为BC上一点,∠CAD=∠B.求证:CA2=CD•CB.(2)、(应用)如图②,在▱ABCD中,P为BC上一点,Q为BA延长线上一点,∠CQP=∠D.若CQ=6,CP=3,求AD的长.(3)、(拓展)如图③,在菱形ABCD中,P是BC上一点,BD∥PQ,BD=2PQ,∠ABC=2∠PAQ,当BP=1,AQ=3 时,请直接写出菱形ABCD的边长.
(1)、(证明)如图①,在△ABC中,D为BC上一点,∠CAD=∠B.求证:CA2=CD•CB.(2)、(应用)如图②,在▱ABCD中,P为BC上一点,Q为BA延长线上一点,∠CQP=∠D.若CQ=6,CP=3,求AD的长.(3)、(拓展)如图③,在菱形ABCD中,P是BC上一点,BD∥PQ,BD=2PQ,∠ABC=2∠PAQ,当BP=1,AQ=3 时,请直接写出菱形ABCD的边长.