河南省南阳市唐河县2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-29 类型:期中考试
一、单选题
-
1. 下列等式成立的是( )A、 B、 C、 D、2. 如图,某超市自动扶梯的倾斜角 为 ,扶梯长 为 米,则扶梯高 的长为( )
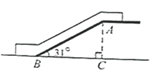 A、 米 B、 米 C、 米 D、 米3. 将方程x2﹣6x+2=0配方后,原方程变形为( )A、(x+3)2=﹣2 B、(x﹣3)2=﹣2 C、(x﹣3)2=7 D、(x+3)2=74. 在 中,最简二次根式的个数为( )A、1个 B、2个 C、3个 D、4个5. 如图,在 中,点D在BC上,连接AD,点E在AC上,过点E作 ,交AD于点F,过点E作 ,交BC于点G,则下列式子一定正确的是( )
A、 米 B、 米 C、 米 D、 米3. 将方程x2﹣6x+2=0配方后,原方程变形为( )A、(x+3)2=﹣2 B、(x﹣3)2=﹣2 C、(x﹣3)2=7 D、(x+3)2=74. 在 中,最简二次根式的个数为( )A、1个 B、2个 C、3个 D、4个5. 如图,在 中,点D在BC上,连接AD,点E在AC上,过点E作 ,交AD于点F,过点E作 ,交BC于点G,则下列式子一定正确的是( )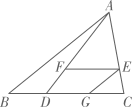 A、 B、 C、 D、6. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A、 B、 C、 D、6. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )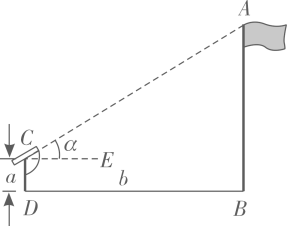 A、 B、 C、 D、7. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根8. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A、 B、 C、 D、7. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根8. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )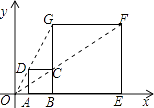 A、(3,2) B、(3,1) C、(2,2) D、(4,2)9. 如图,空地上(空地足够大)有一段长为 的旧墙 ,小敏利用旧墙和木栏围成一个矩形菜园 ,已知木栏总长 ,矩形菜园 的面积为 .若设 ,则可列方程( )
A、(3,2) B、(3,1) C、(2,2) D、(4,2)9. 如图,空地上(空地足够大)有一段长为 的旧墙 ,小敏利用旧墙和木栏围成一个矩形菜园 ,已知木栏总长 ,矩形菜园 的面积为 .若设 ,则可列方程( )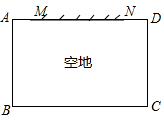 A、 B、 C、 D、10. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( )
A、 B、 C、 D、10. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( )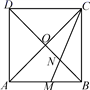 A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
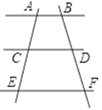
11. 计算: .12. 如图,AB∥CD∥EF,如果AC=2,AE=5,DF=3.6,那么BD=.
 13. 已知 ,则 .14. 如图所示, 是放置在正方形网格中的一个角,则 的值是.
13. 已知 ,则 .14. 如图所示, 是放置在正方形网格中的一个角,则 的值是.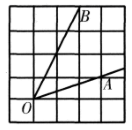 15. 如图,在 中, , , ,E,F分别为 、 上的点,沿直线 将 折叠,使点B恰好落在 上的D处,当 恰好为直角三角形时, 的长为.
15. 如图,在 中, , , ,E,F分别为 、 上的点,沿直线 将 折叠,使点B恰好落在 上的D处,当 恰好为直角三角形时, 的长为.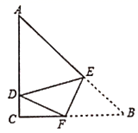
三、解答题
-
16. 计算或解方程:(1)、(2)、(3)、17. 先化简,再求值: ,其中 , .18. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.
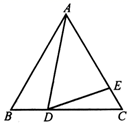 (1)、求证:△ABD∽△DCE;(2)、若BD=4,CE=3,求△ABC的面积.19. 已知关于 的一元二次方程 .(1)、求证:无论 取何值,此方程总有两个不相等的实数根;(2)、若方程有两个实数根 , ,且 ,求 的值.20. 位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
(1)、求证:△ABD∽△DCE;(2)、若BD=4,CE=3,求△ABC的面积.19. 已知关于 的一元二次方程 .(1)、求证:无论 取何值,此方程总有两个不相等的实数根;(2)、若方程有两个实数根 , ,且 ,求 的值.20. 位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水 平步道 上架设测角仪,先在点M处测得观星台最高点A的仰角为 ,然后沿 方向前进 到达点N处,测得点 的仰角为 .测角仪的高度为 ,
(1)、求观星台最高点A距离地面的高度(结果精确到 .参考数据: );(2)、“景点简介”显示,观星台的高度为 ,请计算本次测量结果的误差,并提出一条减小误差的合理化建议.21. 某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.(1)、当每间商铺的年租金定为13万元时,能租出多少间?(2)、当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金﹣各种费用)为275万元?22.(1)、(基础巩固)
如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD•AB.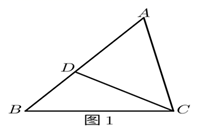 (2)、(尝试应用)
(2)、(尝试应用)如图2,在▱ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
 (3)、(拓展提高)
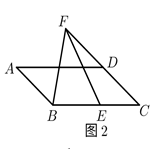
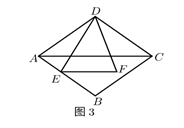
(3)、(拓展提高)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,∠EDF= ∠BAD,AE=2,DF=5,求菱形ABCD的边长.
 23. 如图,已知A,B两点的坐标分别为 , ,点P,Q同时出发分别作匀速运动,其中点P从点A出发沿AO向终点O运动,速度为每秒3个单位长度,点Q从点O出发沿OB运动,速度为每秒2个单位长度,当这两个点有一点到达自己的终点时,另一点也停止运动,设P,Q运动时间为t秒.
23. 如图,已知A,B两点的坐标分别为 , ,点P,Q同时出发分别作匀速运动,其中点P从点A出发沿AO向终点O运动,速度为每秒3个单位长度,点Q从点O出发沿OB运动,速度为每秒2个单位长度,当这两个点有一点到达自己的终点时,另一点也停止运动,设P,Q运动时间为t秒.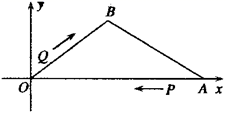 (1)、求t的取值范围;(2)、若以O,P,Q为顶点的三角形与 相似,求此时t的值;(3)、是否存在t,使得 为等腰三角形?若存在,请直接写出运动时间t;若不存在,请说明理由.
(1)、求t的取值范围;(2)、若以O,P,Q为顶点的三角形与 相似,求此时t的值;(3)、是否存在t,使得 为等腰三角形?若存在,请直接写出运动时间t;若不存在,请说明理由.