河南省洛阳市西工区2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，最小的数是（）

A、 $0$ B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
2. 自然界中的数学不胜枚举，如蜜蜂建造的蜂房既坚固又省料，其厚度为0.000073米，将0.000073用科学记数法表示为(（）

A、 $73 \times 10^{﹣ 6}$ B、 $0.73 \times 10^{﹣ 4}$ C、 $7.3 \times 10^{﹣ 4}$ D、 $7.3 \times 10^{﹣ 5}$

查看试题解析
3. 如图，已知 $∠ 1 + ∠ 2 = 180^{°} ， ∠ 3 = 124^{°}$ ，则 $∠ 4$ = （）

A、46° B、56° C、66° D、124°

查看试题解析
4. 如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF形状的变化依次为（）

A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形

查看试题解析
5. 平面直角坐标系中，O为坐标原点，点A的坐标为（ $\sqrt{3}$ ，1），将OA绕原点按逆时针方向旋转90°得OB，则点B的坐标为（）

A、（1， $\sqrt{3}$ ） B、（－1， $\sqrt{3}$ ） C、（0，2） D、（2，0）

查看试题解析
6. 方程x²﹣2x＝0的解是（）

A、0 B、2 C、0或﹣2 D、0或2

查看试题解析
7. 某班学生毕业时，都将自己的照片向本班其他同学送一张留念，全班一共送了1260张，如果全班有x名同学，根据题意，列出方程为（）

A、x（x+1）＝1260 B、2x（x+1）＝1260 C、x（x﹣1）＝1260 D、x（x﹣1）＝1260×2

查看试题解析
8. 如图，抛物线y＝ax²+bx+c交x轴于(﹣1，0)，(3，0)两点，则下列判断中，错误的是（）

A、图象的对称轴是直线x＝1 B、当﹣1＜x＜3时，y＜0 C、当x＞1时，y随x的增大而减小 D、一元二次方程中ax²+bx+c＝0的两个根是﹣1和3

查看试题解析
9. 如果正比例函数 $y = k x (k \neq 0)$ 的图象经过第二、四象限，那么一次函数 $y = k x + k$ 的图象经过（）

A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限

查看试题解析
10. 有两个直角三角形纸板，一个含45°角，另一个含30°角，如图①所示叠放，先将含30°角的纸板固定不动，再将含45°角的纸板绕顶点A顺时针旋转，使BC∥DE ，如图②所示，则旋转角∠BAD的度数为（）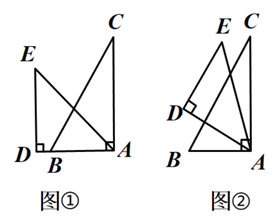

A、15° B、30° C、45° D、60°

查看试题解析

二、填空题

11. 计算 $\sqrt{25}$ ﹣（﹣1）²=

查看试题解析
12. 不等式组 ${\begin{array}{l} x + 4 < 3 \\ \frac{1 - x}{3} \leq 1 \end{array}$ 的解集是．

查看试题解析
13. 二次函数 $y = x^{2} - 4 x - 1$ 的图象的顶点坐标是.

查看试题解析
14. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，下列结论：① $b > 0$ ；② $a - b + c = 0$ ；③一元二次方程 $a x^{2} + b x + c + 1 = 0 (a \neq 0)$ 有两个不相等的实数根；④当 $x < - 1$ 或 $x > 3$ 时， $y > 0$ .上述结论中正确的是.（填上所有正确结论的序号）

查看试题解析
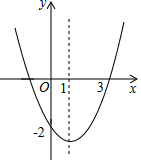15. 如图，矩形ABCD中，AB＝5，BC＝8，点E是边BC上一动点，沿AE把△AEB折叠，得到△AEF，当点F恰好在矩形的对称轴上时，BE的长为.

查看试题解析

三、解答题

16. 先化简（ $\frac{x}{x^{2} + x}$ ﹣1）÷ $\frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ，再求值，其中x是一元二次方程x²﹣3x+2＝0的两根.

查看试题解析
17. 某学校为了解九年级的600名学生每天的自主学习情况，随机抽查了九年级的部分学生，并调查他们每天自主学习的时间.根据调查结果，制作了两副不完整的统计图（图1图2），请根据统计图中的信息回答下列问题：

(1)、本次调查的学生人数是人；

(2)、图2中角 $α$ 是度；

(3)、将图1条形统计图补充完整；

(4)、估算该校九年级学生自主学习不少于1.5小时有多少人.

查看试题解析
18. 如图，一次函数y=kx+b的图象经过（2，4）、（0，2）两点，与x轴相交于点C．求：

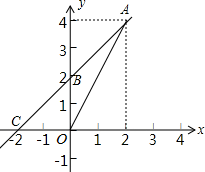(1)、此一次函数的解析式；

(2)、△AOC的面积．

查看试题解析
19. 已知关于x的方程x²﹣8x﹣k²+4k+12＝0.

(1)、求证：无论k取何值，这个方程总有两个实数根；

(2)、若△ABC的两边AB，AC的长是这个方程的两个实数根，第三边BC的长为5，当△ABC是等腰三角形时，求k的值.

查看试题解析
20. 在平面直角坐标系中， $△ A B O$ 的三个顶点坐标分别为 $A (2 ， 3)$ ， $B (3 ， 1)$ ， $O (0 ， 0)$ .

(1)、将 $△ A B O$ 向右平移4个单位，画出平移后的 $△ A_{1} B_{1} O_{1}$ ；

(2)、以点O为对称中心，画出与 $△ A B O$ 成中心对称的 $△ A_{2} B_{2} O$ ，此时四边形 $A B A_{2} B_{2}$ 的形状是；

(3)、在平面上是否存在点D，使得以A，B，O，D为顶点的四边形是平行四边形，若存在，请直接写出符合条件的所有点的坐标；若不存在，请说明理由.

查看试题解析
21. 某学校计划利用一片空地建一个学生自行车车棚，其中一面靠墙，这堵墙的长度为12米.计划建造车棚的面积为80平方米，已知现有的木板材料可使新建板墙的总长为26米.

(1)、为了方便学生出行，学校决定在与墙平行的一面开一个2米宽的门，那么这个车棚的长和宽分别应为多少米？

(2)、如图，为了方便学生取车，施工单位决定在车棚内修建几条等宽的小路，使得停放自行车的面积为54平方米，那么小路的宽为多少米？

查看试题解析
22. 如图1，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点.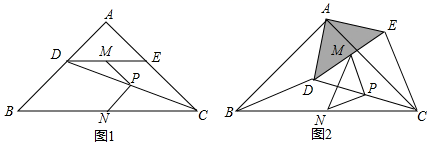

(1)、观察猜想：图1中，线段PM与PN的数量关系是，位置关系是；

(2)、探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；

(3)、拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值.

查看试题解析
23. 如图，已知抛物线 $y = x^{2} + b x + c$ 经过 $A (- 1 ， 0)$ 、 $B (3 ， 0)$ 两点，与y轴相交于点C.

(1)、求抛物线的解析式；

(2)、点P是对称轴上的一个动点，当 $△ P A C$ 的周长最小时，直接写出点P的坐标和周长最小值；

(3)、点Q为抛物线上一点，若 $S_{△ Q A B} = 8$ ，求出此时点Q的坐标.

查看试题解析