河南省安阳市林州市2020-2021学年九年级上学期数学期中考试试卷(B)
试卷更新日期:2021-09-29 类型:期中考试
一、单选题
-
1. 一元二次方程 的解是( )A、 B、3 C、 和3 D、1和22. 已知一元二次方程 有一个根为2,则另一根为( )A、2 B、3 C、4 D、83. 将抛物线 向右平移2个单位长度,再向上平移1个单位长度,得到的抛物线解析式为( )A、 B、 C、 D、4. 服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为( )A、150元 B、160元 C、170元 D、180元5. 已知抛物线 ( ,a,k为常数), , , 是抛物线上三点,则 , , 由小到大依序排列是( )A、 B、 C、 D、6. 若点 与点 关于原点成中心对称,则 的值是( )A、1 B、3 C、5 D、77. 下列图形中,是中心对称图形又是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 8. 如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为 ,则点 的坐标为( )
8. 如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为 ,则点 的坐标为( ) A、 B、 C、 D、9.
A、 B、 C、 D、9.如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )
 A、9 B、7 C、11 D、810. 如图, 与x轴交于点 , ,与 轴的正半轴交于点 .若 ,则点 的纵坐标为( )
A、9 B、7 C、11 D、810. 如图, 与x轴交于点 , ,与 轴的正半轴交于点 .若 ,则点 的纵坐标为( )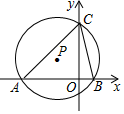 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 当 时, 是二次函数.12. 某旅游景点三月份共接待游客25万人次,五月份共接待游客64万人次,设每月的平均增长率为x,则可列方程为13. 如图,A,B,P是半径为2的 上的三点, ,则弦AB的长为.
 14. 已知扇形的弧长为 ,面积为 ,则扇形的圆心角为.15. 抛物线 经过点 ,该抛物线顶点在直线 上,则该抛物线解析式为.16. 如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C',其中点B的运动路径为 ,则图中阴影部分的面积为.
14. 已知扇形的弧长为 ,面积为 ,则扇形的圆心角为.15. 抛物线 经过点 ,该抛物线顶点在直线 上,则该抛物线解析式为.16. 如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C',其中点B的运动路径为 ,则图中阴影部分的面积为.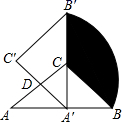 17. 如图,在 中, , , ,以AC为腰,点A为顶点作等腰 ,且 ,则 .
17. 如图,在 中, , , ,以AC为腰,点A为顶点作等腰 ,且 ,则 .
三、解答题
-
18. 解下列方程:(1)、 ;(2)、19. 已知关于x的方程 .(1)、求证:无论m取何值,方程总有两个不相等的实数根;(2)、若此方程的一个根是1,请求出m的值及方程的另一个根,并求以此两根作为两边的等腰三角形(不是等边三角形)的周长.20. 如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
 (1)、求圆弧所在的圆的半径r的长;(2)、当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
(1)、求圆弧所在的圆的半径r的长;(2)、当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
21. 如图所示,AB为半圆O的直径,C为圆上一点,AD平分∠BAC交半圆于点D,过点D作DE⊥AC,DE交AC的延长线于点E. (1)、求证:DE是⊙O的切线;(2)、若⊙O的半径为2,DE= ,求线段AC的长22. 某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
(1)、求证:DE是⊙O的切线;(2)、若⊙O的半径为2,DE= ,求线段AC的长22. 某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:销售单价x(元)
85
95
105
115
日销售量y(个)
175
125
75
m
日销售利润w(元)
875
1875
1875
875
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)、求y关于x的函数解析式(不要求写出x的取值范围)及m的值;(2)、根据以上信息,填空:该产品的成本单价是元,当销售单价x=元时,日销售利润w最大,最大值是元;
(3)、公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?23. 小强根据学习函数的经验,对函数 ;图象与性质进行了探究,下面是小强的探究过程,请补充完整,并解决相关问题: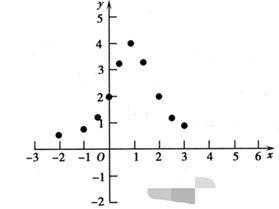 (1)、函数 ;的自变量x的取值范围是;(2)、如表是y与x的几组对应值.
(1)、函数 ;的自变量x的取值范围是;(2)、如表是y与x的几组对应值.x
m
0
1
2
3
4
y
2
4
2
n
表中m的值为 , n的值为;
(3)、如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数 的大致图象;(4)、结合函数图象,请写出函数 的一条性质:.(5)、解决问题:如果方程 的实数根有2个,那么a的取值范围是.24. 已知 , , 是过点A的直线,过点D作 于B,连接 . (1)、问题发现:如图①,过点C作 ,与 交于点E,则容易发现 与 之间的数量关系为 , , , 之间的数量关系为.(2)、拓展探究:当 绕点A旋转到如图②的位置时,试猜想线段 , , 之间的数量关系,并证明;(3)、解决问题:当 绕点A旋转到如图③的位置时(点C,D在直线 的两侧),若此时 , ,则 .25. 如图,抛物线 与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)、问题发现:如图①,过点C作 ,与 交于点E,则容易发现 与 之间的数量关系为 , , , 之间的数量关系为.(2)、拓展探究:当 绕点A旋转到如图②的位置时,试猜想线段 , , 之间的数量关系,并证明;(3)、解决问题:当 绕点A旋转到如图③的位置时(点C,D在直线 的两侧),若此时 , ,则 .25. 如图,抛物线 与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.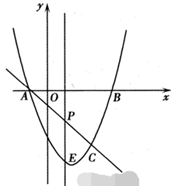 (1)、求A、B两点的坐标及直线AC的函数表达式;(2)、P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)、点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
(1)、求A、B两点的坐标及直线AC的函数表达式;(2)、P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)、点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.