黑龙江省哈尔滨市五常市2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-09-29 类型:期末考试
一、单选题
-
1. 5的相反数是( ).A、 0.2 B、5 C、 D、2. 如图,对于直线 ,线段 ,射线 ,其中能相交的是( ).A、
 B、
B、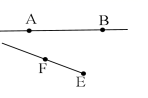 C、
C、 D、
D、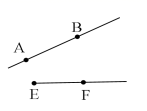 3. 我省土地总面积为473000平方千米,这个数用科学记数法表示正确的是( )A、 B、 C、 D、4. 已知 与 的和是单项式,则 的值是( )A、5 B、6 C、7 D、85. 下列平面图形中不能围成正方体的是( )
3. 我省土地总面积为473000平方千米,这个数用科学记数法表示正确的是( )A、 B、 C、 D、4. 已知 与 的和是单项式,则 的值是( )A、5 B、6 C、7 D、85. 下列平面图形中不能围成正方体的是( )
A、 B、
B、 C、
C、 D、
D、 6. 方程 ,去分母得( )A、 B、 C、 D、7. 用一副三角板不能画出的角是( ).A、75° B、105° C、110° D、135°8. 下面左边是用八块完全相同的小正方体搭成的几何体,从正面看该几何体得到的图是( )
6. 方程 ,去分母得( )A、 B、 C、 D、7. 用一副三角板不能画出的角是( ).A、75° B、105° C、110° D、135°8. 下面左边是用八块完全相同的小正方体搭成的几何体,从正面看该几何体得到的图是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 一件毛衣先按成本提高50%标价,再以8折出售,获利28元,求这件毛衣的成本是多少元,若设成本是x元,可列方程为( )A、0.8x+28=(1+50%)x B、0.8x﹣28=(1+50%)x C、x+28=0.8×(1+50%)x D、x﹣28=0.8×(1+50%)x10. 有如下说法:①射线 与射线 表示同一射线;②用一个扩大3倍的放大镜去看一个角,这个角扩大3倍;③两点之间,线段最短;④两点确定一条直线;其中正确的有( ).A、5个 B、4个 C、3个 D、2个
9. 一件毛衣先按成本提高50%标价,再以8折出售,获利28元,求这件毛衣的成本是多少元,若设成本是x元,可列方程为( )A、0.8x+28=(1+50%)x B、0.8x﹣28=(1+50%)x C、x+28=0.8×(1+50%)x D、x﹣28=0.8×(1+50%)x10. 有如下说法:①射线 与射线 表示同一射线;②用一个扩大3倍的放大镜去看一个角,这个角扩大3倍;③两点之间,线段最短;④两点确定一条直线;其中正确的有( ).A、5个 B、4个 C、3个 D、2个二、填空题
-
11. 在数学知识抢答赛中,如果用 分表示得10分,那么扣20分表示为.12. 已知1是关于x的方程 的解,则 .13. 若a、b是互为倒数,则2ab﹣5= .14. 比较大小: (填“>”或“<”号)15. 若关于 的多项式 不含 项,则 .16. 某车间有21名工人,每人每天可以生产螺栓12个或螺母18个,设 名工人生产螺栓,其他工人生产螺母,要求每天生产的螺栓和螺母按 刚好配套,则可列方程为 .17. 已知方程 ,用含y的代数式表示x,则 .18. 小明和小莉出生于1998年12月份,他们的出生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期之和是36(不算年份、月份),那么小莉的出生日期是12月日.19. 将一副三角板如图放置,若 ,则 的大小为 .
 20. 已知线段 , ,点 在直线 上,点 分别是线段 的中点,则线段 的长= .
20. 已知线段 , ,点 在直线 上,点 分别是线段 的中点,则线段 的长= .三、解答题
-
21. 计算下列各题:(1)、(2)、22. 解下列方程:(1)、(2)、23. 计算(1)、(2)、 ,其中 .24. 出租车司机小王每天下午的营运全都是在东西走向的人民大街进行的,如果规定向东为正、向西为负,他这天下午共运行11次,行车里程如下:(单位: )
+15、 ,问:
(1)、将最后一名乘客送到目的地时,小王距离下午出车时的地点有多千米?(2)、若汽车耗油量为a升/千米,这天下午小王共耗油多少升?(3)、判断一下:人民大街的总长度不能小于多少千米?(4)、小王所开的出租车按物价部门规定:起步价5元(即:不超过 ,收5元),超过 后,每行驶1千米加价1元,小王这天下午共收入多少元(不计算耗油钱)?25. 列方程解应用题修一条公路,甲队单独修需要10天完成,乙队单独修需要12天完成,丙队单独修需要15天完成.现在先由甲队修2.5天,再由乙队接着修,最后还剩下一段路,由三队合修2天才完成任务.求乙队在整个修路工程中工作的天数.
26.(1)、如图,从O点引出6条射线 ,且 , 、 分别是 的平分线.则 的度数为度 (2)、钟面上的时间是3点整,然后,时针与分针继续正常行走,当分针与时针的夹角成 时,针指向3点到4点之间,求此时刻是几点几分.(3)、一个角的余角比这个角的补角的一半小 ,则这个角的度数为度27. 在数轴上原点O表示数0,A点表示的数是m,B点表示的数是n,并且满足 .(1)、点A表示的数为 , 点B表示的数为;(2)、若动点P从点A出发,以每秒3个单位长度的速度沿数轴向右运动;同时动点Q从点B出发以每秒2个单位长度的速度沿数轴向左运动.设P运动的时间为t秒,并且 两点在C点相遇.试求t值及C点所表示的数;(3)、在(2)的条件下,若点P运动到达B点后按原速立即返回,点Q继续按原速原方向运动,点P离开B点多少秒后, 两点的距离为4个单位长度?
(2)、钟面上的时间是3点整,然后,时针与分针继续正常行走,当分针与时针的夹角成 时,针指向3点到4点之间,求此时刻是几点几分.(3)、一个角的余角比这个角的补角的一半小 ,则这个角的度数为度27. 在数轴上原点O表示数0,A点表示的数是m,B点表示的数是n,并且满足 .(1)、点A表示的数为 , 点B表示的数为;(2)、若动点P从点A出发,以每秒3个单位长度的速度沿数轴向右运动;同时动点Q从点B出发以每秒2个单位长度的速度沿数轴向左运动.设P运动的时间为t秒,并且 两点在C点相遇.试求t值及C点所表示的数;(3)、在(2)的条件下,若点P运动到达B点后按原速立即返回,点Q继续按原速原方向运动,点P离开B点多少秒后, 两点的距离为4个单位长度?