黑龙江省大庆市龙凤区2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-09-29 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列大学的校徽图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,下列条件中能得到AB∥CD的是( )
3. 如图,下列条件中能得到AB∥CD的是( )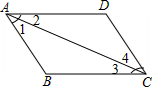 A、 B、 C、 D、4. 在一个不透明的口袋中装有若干个颜色不同其余都相同的球,如果口袋中装有3个红球且摸到红球的频率为 , 那么口袋中球的总个数为( )A、13 B、14 C、15 D、165. 若等腰三角形的一个内角为80°,则这个等腰三角形的顶角为( )A、80° B、50° C、80°或50° D、80°或20°6. 如图, , , 于点E, 于点D, , ,则 的长是( )
A、 B、 C、 D、4. 在一个不透明的口袋中装有若干个颜色不同其余都相同的球,如果口袋中装有3个红球且摸到红球的频率为 , 那么口袋中球的总个数为( )A、13 B、14 C、15 D、165. 若等腰三角形的一个内角为80°,则这个等腰三角形的顶角为( )A、80° B、50° C、80°或50° D、80°或20°6. 如图, , , 于点E, 于点D, , ,则 的长是( )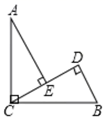 A、 B、 C、 D、7. 已知汽车油箱内有油50L , 每行驶100km耗油10L , 那么汽车行驶过程中油箱内剩余的油量Q(L)与行驶路程S(km)之间的关系式是( )A、Q=50﹣ B、Q=50+ C、Q=50﹣ D、Q=50+8. 如图,直线是一条河, 、 是两个新农村定居点.欲在 上的某点处修建一个水泵站,直接向 、 两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( )
A、 B、 C、 D、7. 已知汽车油箱内有油50L , 每行驶100km耗油10L , 那么汽车行驶过程中油箱内剩余的油量Q(L)与行驶路程S(km)之间的关系式是( )A、Q=50﹣ B、Q=50+ C、Q=50﹣ D、Q=50+8. 如图,直线是一条河, 、 是两个新农村定居点.欲在 上的某点处修建一个水泵站,直接向 、 两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( )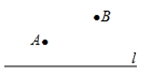 A、
A、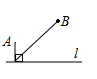 B、
B、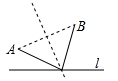 C、
C、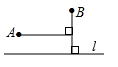 D、
D、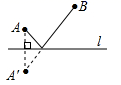 9. 下列说法中,错误的有( )
9. 下列说法中,错误的有( )①不在角的平分线上的点到这个角的两边的距离不相等;
②三角形两内角的平分线的交点到各边的距离相等;
③到三角形三边距离相等的点有1个
④线段中垂线上的点到线段两端点的距离相等,
⑤到三角形三个顶点距离相等的点有1个
A、0个 B、1个 C、2个 D、3个10. 已知∠AOB=30°,点P在∠AOB的内部,点P1和点P关于OA对称,点P2和点P关于OB对称,则P1、O、P2三点构成的三角形是( )A、直角三角形 B、钝角三角形 C、等腰直角三角形 D、等边三角形二、填空题
-
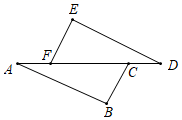
11. 若(x+2)(x﹣4)=x2+nx﹣8,则n= .12. 如图所示,已知AF=DC,BC∥EF,若要用“ASA”去证△ABC≌△DEF,则需添加的条件是 .
 13. 如图所示,△ABC中,AB=6,AC=8,沿过B点的直线折叠这个三角形,使点A落在BC边上的点E处,折痕为BD . 若△CDE的周长为11,则BC长为 .
13. 如图所示,△ABC中,AB=6,AC=8,沿过B点的直线折叠这个三角形,使点A落在BC边上的点E处,折痕为BD . 若△CDE的周长为11,则BC长为 .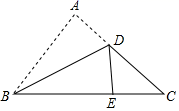 14. 等腰三角形周长为20,一边长为4,则另两边长为 .15. 已知等腰△ABC,其腰上的高线与另一腰的夹角为35°,那么顶角为度数是.16. 如图,∠BAC=108°,若MP 和NQ 分别垂直平分AB 和AC , 则∠PAQ 的度数是 .
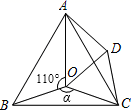
14. 等腰三角形周长为20,一边长为4,则另两边长为 .15. 已知等腰△ABC,其腰上的高线与另一腰的夹角为35°,那么顶角为度数是.16. 如图,∠BAC=108°,若MP 和NQ 分别垂直平分AB 和AC , 则∠PAQ 的度数是 .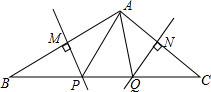 17. 等边三角形的两条中线所夹的锐角的度数为18. 中, 是直角,O是两内角平分线的交点, , , ,O到三边的距离是.
17. 等边三角形的两条中线所夹的锐角的度数为18. 中, 是直角,O是两内角平分线的交点, , , ,O到三边的距离是. 19. 如图,已知, 、 分别平分 和 且 度,则 度.
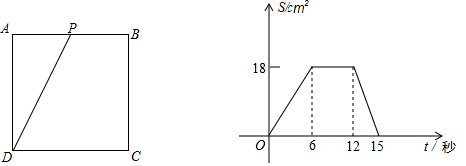
19. 如图,已知, 、 分别平分 和 且 度,则 度. 20. 甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.若丙也从甲出发的地方沿相同的方向骑自行车行驶,且与甲的速度相同,当甲追上乙后45秒时,丙也追上乙,则丙比甲晚出发秒.
20. 甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.若丙也从甲出发的地方沿相同的方向骑自行车行驶,且与甲的速度相同,当甲追上乙后45秒时,丙也追上乙,则丙比甲晚出发秒.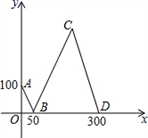
三、解答题
-
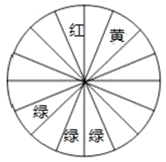
21. 计算:22. 某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转动停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得100元、50元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券15元.转转盘和直接获得购物券,你认为哪种方式更合算?
 23. 如图,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AD于点E,EF⊥ AB,垂足为F. 求证:EF=ED.
23. 如图,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AD于点E,EF⊥ AB,垂足为F. 求证:EF=ED.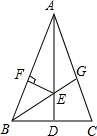 24. 如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.
24. 如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.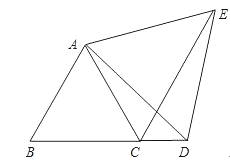 25. 如图,在 中, ,D、A、E三点都在直线m上,并且有 ,求证: .
25. 如图,在 中, ,D、A、E三点都在直线m上,并且有 ,求证: .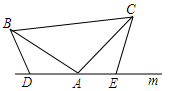 26. 已知:在 和 中, , .如图,若 ,试探究 与 的关系,并说明理由
26. 已知:在 和 中, , .如图,若 ,试探究 与 的关系,并说明理由