黑龙江省齐齐哈尔市龙沙区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-29 类型：期末考试

进入出卷网下载

一、单选题

1. 已知抛物线 $y = x^{2} - x - 1$ 与x轴的一个交点为 $(m ， 0)$ ，则代数式 $m^{2} - m + 2020$ 的值为（）

A、2018 B、2019 C、2020 D、2021

查看试题解析
2. 下列图形中，中心对称图形有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 李明参加的社区抗疫志愿服务团队共有A、B、C、D四个服务项目，其中每个服务项目又分为第一小组和第二小组，则李明分到A项目的第一小组的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{3}{8}$

查看试题解析
4. 已知蓄电池的电压为定值．使用电池时，电流I（A）与电阻R（Ω）是反比例函数关系，图象如图所示．如果以此蓄电池为电源的电器的限制电流不能超过3A，那么电器的可变电阻R（Ω）应控制在（）

A、R≥1 B、0＜R≤2 C、R≥2 D、0＜R≤1

查看试题解析
5. 为测量某地温度变化情况，记录了一段时间的温度．一段时间内，温度y与时间t的函数关系满足y =-t²+12t+2，当4≤ t ≤8时，该地区的最高温度是（）

A、38℃ B、37℃ C、36℃ D、34℃

查看试题解析
6. 如图， $△ A B C$ 中，∠B＝90°，AB＝BC＝4cm，点D为AB中点，点E和点F同时分别从点D和点C出发，沿AB、CB边向点B运动，点E和点F的速度分别为1cm/s和2cm/s，则 $△ A E F$ 的面积ycm²与点F运动时间x/s之间的函数关系的图象大致为（）

A、 B、 C、 D、

查看试题解析
7. 如图，在 $△ A B C$ 中，∠BAC＝90°，AD⊥BC，垂足为点D，下列结论错误的是（）

A、AB²＝BD·BC B、AC²＝DC·BC C、AD²＝BD·DC D、BC²＝AB·AC

查看试题解析
8. 如图，在 $⊙ O$ 中，弦 $A B$ 所对的圆周角 $∠ C = 45 °$ ， $A B = \sqrt{2}$ ， $B C = 1$ ，则 $∠ A$ 度数为（）

A、 $60 °$ B、 $45 °$ C、 $36 °$ D、 $30 °$

查看试题解析
9. 如图， $△ A B C$ 的顶点都是正方形网格中的格点，则sin∠CAB等于（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、2

查看试题解析
10. 如图，抛物线y＝ax²+bx+c（a≠0）的对称轴为x＝1，与x轴交于A、B（3，0）两点，与y轴交于点C，连接AC．有下列四个结论：①bc＜0；②b＝2a；③a+b≥am²+bm（m为任意实数）；④将直线AC向下平移|c|个单位长度得到的直线与直线AC向右平移1个单位长度得到的直线重合．其中正确结论的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 抛物线y＝x²+2x+m顶点在第二象限，则m的取值范围是．

查看试题解析
12. 如图，四边形ABCD的对角线AC与BD交于点O，AC⊥BD，且AC平分BD，若添加一个条件，则四边形ABCD为菱形．

查看试题解析
13. 点C在线段AB上，AB＝1cm，若AC²＝AB·BC，那么线段AC的长为cm．（结果用无理数表示）

查看试题解析
14. 由若干个相同的小正方体搭成的几何体的三视图相同，如图所示．至少再加个小正方体，该几何体可成为一个正方体．

查看试题解析
15. 如图，在平面直角坐标系中，点A（0，8），点B（8，0），点C在线段AB上，AC＝2 $\sqrt{2}$ ，若以原点O为位似中心，把线段AB缩小为原来的 $\frac{1}{2}$ ，得到线段 $A^{'} B^{'}$ ，则点C的对应点 $C^{'}$ 坐标为．

查看试题解析
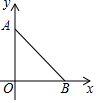16. 如图所示，第二象限内的点A，B在反比例函数y＝ $\frac{k}{x}$ （k≠0），的图象上，∠ACO＝∠ADB＝90°，∠AOC＝45°，tan∠BAD＝3，BD＝6，则OA长为．

查看试题解析
17. 如图，在 $△ A B C$ 中，∠A＝90°，AB＝2²⁰²¹ ， AC＝2²⁰²⁰ ，点D₁ ， D₃ ， D₅ ， …D_2n_﹣1在AB边上，点D₂ ， D₄ ， D₆ ， …D_2n在AC边上，若∠B＝∠ACD₁＝∠AD₁D₂＝∠AD₂D₃＝…＝∠AD_nD_n+1 ，则D₂₀₂₀D₂₀₂₁＝．

查看试题解析

三、解答题

18.

(1)、计算：2tan60°·tan30°﹣4cos²45°+sin60°；

(2)、如图，在△ABC中，tanC＝ $\frac{3}{5}$ ，点D在边BC上，AB＝AD，CD＝2BD＝4，求sinB的值．

查看试题解析
19. 解方程：（x+1）²﹣4＝3（x+1）．

查看试题解析
20. 如图，以AC为直径的⊙O与 $△ A B C$ 的AB、BC两边分别交于D、E两点，AB＝AC，EF⊥AB，垂足为F，延长FE与AC交于点G．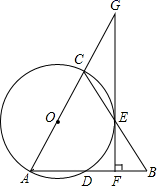

(1)、求证：EF是⊙O的切线；

(2)、若AC＝2CE，则cosG为．

查看试题解析
21. 新冠疫情期间，口罩的需求量增大，某口罩加工厂承揽生产1600万个口罩的任务，每天生产的口罩数量相同，计划用x天（x＞4）完成．

(1)、求每天生产口罩y（万个）与生产时间x（天）之间的函数表达式；

(2)、由于疫情形势严峻，卫生管理部门要求厂家提前4天交货，那么加工厂每天要多做20万个口罩才能完成任务，求实际生产时间．

查看试题解析
22. 如图，某建筑AB与山坡CD的剖面在同一平面内，在距此建筑AB楼底B点左侧水平距离60m的C点处有一个山坡，山坡CD的坡度i＝1：0.75，山坡坡底C点到坡顶D点的距离CD＝50m，在坡顶D点处测得建筑楼顶A点的仰角为30°，求此建筑AB的高度．（结果用无理数表示）

查看试题解析
23. 如图1，在 $R t △ A B C$ 中，∠C＝90°，将 $△ A B C$ 绕点A逆时针旋转90°得到 $△ A E D$ ．延长ED分别交CB于点F，交AB于点G，连接AF．

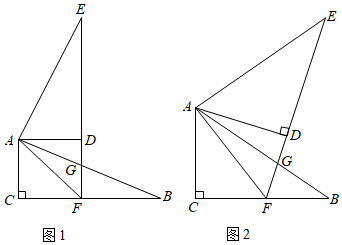(1)、∠CAF＝°，∠EAG＝°；

(2)、若BC＝（ $\sqrt{2}$ +1）AC，则①∠DAG＝ ▲ °；② $\frac{F G}{G D}$ ＝ ▲ ，请证明你的结论；

(3)、如图2，若改变旋转角，已知AC＝3，BC＝4，当∠EAF＝90°时，求 $△ A F B$ 的面积．

查看试题解析
24. 在图1中，抛物线y＝ax²+2ax﹣8（a≠0）与x轴交于点A、B（点A在B左侧），与y轴负半轴交于点C，OC＝4OB，连接AC，抛物线的对称轴交x轴于点E，交AC于点F．

(1)、AB的长为， a的值为；

(2)、图2中，直线ON分别交EF、抛物线于点M、N，OM＝ $\sqrt{17}$ ，连接NC．
①求直线ON的解析式；

②证明：NC∥AB；

③第四象限存在点P使 $△ B F P$ 与 $△ A O C$ 相似，且BF为 $△ B F P$ 的直角边，请直接写出点P坐标．

查看试题解析