黑龙江省齐齐哈尔市建华区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列球类小图标中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知x＝1是一元二次方程x²﹣2mx+1＝0的一个解，则m的值是（）

A、1 B、0 C、0或1 D、0或﹣1

查看试题解析
3. 如图，⊙O的半径为1，A，B，C是圆周上的三点，∠BAC=36°，则劣弧BC的长是（）

A、 $\frac{1}{5} π$ B、 $\frac{2}{5} π$ C、 $\frac{3}{5} π$ D、 $\frac{4}{5} π$

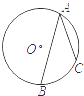查看试题解析
4. 下列命题中正确的个数为（）
①一个角对应相等的两个等腰三角形相似

②两边对应成比例且一个角对应相等的两个三角形相似

③一个锐角对应相等的两个直角三角形相似

④三边对应成比例的两个三角形相似

A、1 B、2 C、3 D、4

查看试题解析
5. 在平面直角坐标系内 $P$ 点的坐标（ $\cos 30 °$ ， $\tan 45 °$ ），则 $P$ 点关于 $x$ 轴对称点 $P_{1}$ 的坐标为（）

A、 $(\frac{\sqrt{3}}{2} ， 1)$ B、 $(- 1 ， \frac{\sqrt{3}}{2})$ C、 $(\frac{\sqrt{3}}{2} ， - 1)$ D、 $(- \frac{\sqrt{3}}{2} ， - 1)$

查看试题解析
6. 如图，D，E分别是AB，AC上两点，CD与BE相交于点O，下列条件中不能使△ABE和△ACD相似的是（）

A、∠B=∠C B、∠ADC=∠AEB C、BE=CD，AB=AC D、AD：AC=AE：AB

查看试题解析
7. 用一块长80cm、宽60cm的矩形薄钢片，在四个角上截去四个相同的边长为 $x$ cm的小正方形，然后做成底面积为 $1500 {cm}^{2}$ 的没有盖的长方体盒子，为求出 $x$ ，根据题意列方程并整理后得（）

A、 $x^{2} - 70 x + 875 = 0$ B、 $x^{2} + 70 x - 825 = 0$ C、 $x^{2} - 70 x - 825 = 0$ D、 $x^{2} - 70 x + 825 = 0$

查看试题解析
8. 一船向东航行，上午8时到达 $B$ 处，观测到有一灯塔在它的南偏东60°且距离为72海里的 $A$ 处，上午10时到达 $C$ 处，此时观测到灯塔在它的正南方向，则这艘船航行的速度为（）

A、18海里/小时 B、 $18 \sqrt{3}$ 海里/小时 C、36海里/小时 D、 $36 \sqrt{3}$ 海里/小时

查看试题解析
9. 已知关于 $x$ 的一元二次方程 ${(m - 1)}^{2} x^{2} + (2 m - 1) x + 1 = 0$ 有两个不相等的实数根，则 $m$ 的取值范围是（）

A、 $m > \frac{3}{4}$ B、 $m \geq \frac{3}{4}$ C、 $m > \frac{3}{4}$ 且 $m \neq 1$ D、 $m \geq \frac{3}{4}$ 且 $m \neq 1$

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，给出下列五个式子：① $a c$ ；② $a + b + c$ ；③ $4 a - 2 b + c$ ；④ $2 a + b$ ；⑤ $2 a - b$ ．其中值大于0的式子有（）个．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 如果 $x = 2$ 是一元二次方程 $2 x^{2} - 2 x = a^{2}$ 的一个根，则常数 $a$ 的值是．

查看试题解析
12. 在一个袋子里装有10个球，6个红球，3个黄球，1个绿球，这些球除颜色外、形状、大小、质地等都完全相同，充分搅匀后，在看不到球的条件下，随机从这个袋子中摸出一球，摸出红球的概率是．

查看试题解析
13. 如图， $P A$ 与 $⊙ O$ 相切，切点为 $A$ ， $P O$ 交 $⊙ O$ 于点 $C$ ，点 $B$ 是优弧 $C B A$ 上一点，若 $∠ A B C = 28 °$ ，则 $∠ P$ 的度数为．

查看试题解析
14. 若 $\sqrt{3}$ tan（x+10°）=1，则锐角x的度数为．

查看试题解析
15. 若正比例函数 $y = 2 k x$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于点 $A (m ， 1)$ ，则 $k$ 的值是．

查看试题解析
16. 如图，⊙O的半径为2，点A的坐标为（2，2 $\sqrt{3}$ ），直线AB为⊙O的切线，B为切点．则B点的坐标为．

查看试题解析
17. 如图，矩形 $A B C O$ 的对角线 $A C$ 、 $O B$ 交于点 $A_{1}$ ，直线 $A C$ 的解析式 $y = - \sqrt{3} x + \sqrt{3}$ ，过点 $A_{1}$ 作 $A_{1} O_{1} ⊥ O C$ 于 $O_{1}$ ，过点 $A_{1}$ 作 $A_{1} B_{1} ⊥ B C$ 于 $B_{1}$ ，得到第二个矩形 $A_{1} B_{1} C O_{1}$ ， $A_{1} C$ 、 $O_{1} B_{1}$ 交于点 $A_{2}$ ，过点 $A_{2}$ 作 $A_{2} O_{2} ⊥ O C$ 于 $O_{2}$ ，过点 $A_{2}$ 作 $A_{2} B_{2} ⊥ B C$ 于 $B_{2}$ ，得到第三个矩形 $A_{2} B_{2} C O_{2}$ ，…，依此类推，这样作的第 $n$ 个矩形对角线交点 $A_{n}$ 的坐标为．

查看试题解析

三、解答题

18.

(1)、解方程 $x (x - 2) = 3$

(2)、计算： $- 1^{4} + \sqrt{12} \sin 60 ° - {(\frac{1}{2})}^{- 1} + {(3 - π)}^{0}$

查看试题解析
19. 如图，在平面直角坐标系中，一次函数 $y = k_{1} x + b$ 与反比例函数 $y = \frac{k_{2}}{x}$ 的图象交于 $A (1 ， 6)$ 、 $B (a ， 3)$ 两点．

(1)、求一次函数 $y = k_{1} x + b$ 与反比例函数 $y = \frac{k_{2}}{x}$ 的解析式；

(2)、如图，点 $D$ 在 $x$ 轴上，四边形 $O B C D$ 中， $B C$ ∥ $O D$ ， $O B$ 与 $D C$ 不平行， $O B = D C$ ，过点 $C$ 作 $C E ⊥ O D$ 于点 $E$ ， $C E$ 和反比例函数的图象交于点 $P$ ，当四边形 $O B C D$ 的面积为18时， $B C =$ ， $P E ： P C$ 的值为．

查看试题解析
20. 如图，长方形绿地长32m、宽20m，要在这块绿地上修建宽度相同且与长方形各边垂直的三条道路，使六块绿地面积共 $570 m^{2}$ ，问道路宽应为多少？

查看试题解析
21. 如图， $△ A B C$ 中， $C D$ 是边 $A B$ 上的高，且 $\frac{A D}{C D} = \frac{C D}{B D}$ ．

(1)、求证： $∠ A C B = 90 °$ ；

(2)、若 $A C = 3$ ， $\sin ∠ C A B = \frac{4}{5}$ ，求 $D B$ 的长．

查看试题解析
22. 在一个不透明的口袋中装有4张相同的纸牌，它们分别标有数字1，2，3，4．随机地摸取出一张纸牌然后放回，在随机摸取出一张纸牌，

(1)、计算两次摸取纸牌上数字之和为5的概率；

(2)、甲、乙两个人进行游戏，如果两次摸出纸牌上数字之和为奇数，则甲胜；如果两次摸出纸牌上数字之和为偶数，则乙胜．这是个公平的游戏吗？请说明理由．

查看试题解析
23. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $D$ 是 $A B$ 边上的一点， $B D$ 为直径的 $⊙ O$ 与边 $A C$ 相切于点 $E$ ，连结 $D E$ 并延长，与 $B C$ 的延长线交于点 $F$ ．

(1)、求证： $B D = B F$ ；

(2)、若 $B C = 6$ ， $A D = 4$ ，求 $B F$ 的长．

查看试题解析
24. 如图所示，二次函数 $y = - x^{2} + 2 x + m$ 的图象与 $x$ 轴的一个交点为 $A (3 ， 0)$ ，另一个交点为 $B$ ，且与 $y$ 轴交于点 $C$ ．

(1)、求 $m$ 的值；

(2)、求点 $B$ 的坐标；

(3)、该二次函数图象上有一点 $D (x ， y)$ （其中 $x > 0$ ， $y > 0$ ），使 $S_{△ A B D} = S_{△ A B C}$ ，求点 $D$ 的坐标；

(4)、若点 $P$ 在直线 $A C$ 上，点 $Q$ 是平面上一点，是否存在点 $Q$ ，使以点 $A$ 、点 $B$ 、点 $P$ 、点 $Q$ 为顶点的四边形为矩形？若存在，请你直接写出 $Q$ 点的坐标；若不存在，请说明理由．

查看试题解析